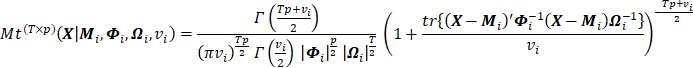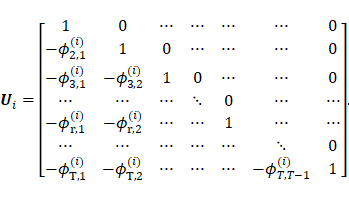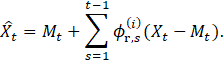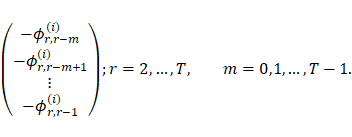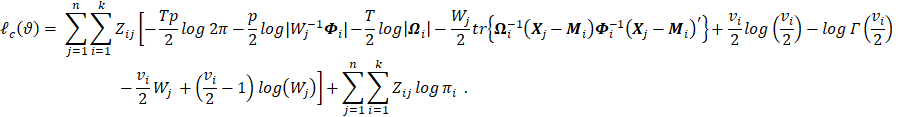Journal of Machine Intelligence and Data Science (JMIDS)

1. Introduction

Finite mixture models in the statistical data analysis mainly contribute to modelling a heterogeneous population and providing an easy and model-based method for clustering and classification structure [1], [2].

Different studies have evaluated various finite mixtures of distributions focusing on multivariate (two-way data) distributions. For instance, such studies have proposed different finite mixtures of multivariate distributions, including multivariate normal distribution, multivariate t-distribution [3], multivariate skew-normal distribution [4], multivariate skew-t-distribution [5], multivariate normal inverse Gaussian [6], multivariate generalized hyperbolic distribution [7], and multivariate power exponential distribution [8] over the last two decades.

Three-way data including multivariate longitudinal, spatial multivariate, and spatio-temporal data may be available in a range of scientific domains [9]. Despite the important role of matrix-variate distributions in three-way data analysis, a small body of research exists in this respect. For example, Viroli (2011) introduced the finite mixtures of matrix-variate normal distributions (MVNDs) for classifying the three-way data. In addition, Anderlucci and Viroli (2015a) considered the finite mixture of MVNDs for multivariate longitudinal data. In another study, Doğru, Bulut and Arslan (2016) proposed a finite mixture of matrix-variate t-distributions (MVTDs). Further, Gallaugher and McNicholas (Gallaugher and McNicholas, 2017a; Gallaugher and McNicholas, 2017b; Gallaugher and McNicholas, 2019) applied four skewed matrix-variate distributions of matrix-variate skew-t, generalized hyperbolic, variance-gamma, and normal inverse Gaussian distributions in the finite mixture of these distributions. Too, Tomarchio (2024) presented the matrix-variate normal mean-variance Birnbaum–Saunders distribution and mixture of it in the model-based clustering.

In the two- or three-way data, where there are some departures from normality in datasets, using normal distributions affects the estimation of some parameters (McNicholas and Murphy 2010). The presence of outlier or heavy-tailed data is considered as one of the common departures from normality and in such case, the mixture of t-distributions is an appropriate alternative to the mixture of normal distributions [12].

On the other hand, without any constraints on mixture parameters, the number of estimated parameters increases dramatically by an increase in components. Therefore, some constraints should be put on model parameters in order to achieve more parsimonious models. Considering a large number of mixture parameters in the covariance matrix component, more attention should be drawn on covariance structure decomposition. Further literature contains parsimonious covariance matrices in the mixture of multivariate distributions (Banfield and Raftery, 1993; Celeux and Govaert, 1995; Fraley and Raftery, 2002; McNicholas and Murphy, 2010; Andrews and McNicholas, 2012; McNicholas and Subedi, 2012; Vrbik and McNicholas, 2014).

Some studies have investigated the parsimonious feature only in the finite mixture of MVNDs for three-way (Viroli, 2011; L Anderlucci and Viroli, 2015a; Sarkar et al., 2020). However, Tomarchio (2023) applied a parsimonious MVTD mixture model through the eigenvalue decomposition  of two covariance matrices. To the best of our knowledge, no research has applied the parsimonious MVTD mixture model to multivariate longitudinal data. Therefore, the present study focused on the parsimonious mixture of MVTDs for clustering multivariate longitudinal data with outliers or heavy-tails. The remaining sections of the present study are organized as follows. Section 2 reviews the finite mixture of MVTDs and the decomposition of covariance matrices. Further, the details of the estimates of MVTD parameters are provided in Section 3. Furthermore, Section 4 discusses the simulation studies and real examples in order to demonstrate the performance of models, followed by presenting the main findings in Section 5.

2. Background

2.1 Finite mixture of MVTDs

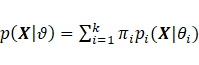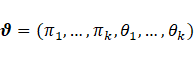A  dimensional random matrix X is assumed to arise from a parametric finite mixture if it is possible to write  for all , where  is the vector of parameters, and  and k are the mixing proportion and the number of mixture components, respectively, so that 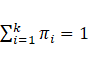 and 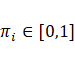. Additionally,  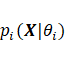is referred to as the density of the i^th component. In the mixture of MVTDs, component density with a  mean matrix , two covariance matrices and  with dimensions  and , and degrees of freedom  is as follows [27]:

(1)

where T and p indicate the number of measurement times and the number of response variables, respectively. In addition,  and  are commonly referred to as between and within covariance matrices, respectively. In the present study, the upper case boldface was used for the matrices.

The MVTDs arise as a particular case of a normal variance mixture distribution. In this formulation, the random matrix X is defined as [12]:

(2)

where the matrix random V has the MVND with the mean matrix 0 and covariance matrices  and , , and the latent random variable W follows a gamma distribution with parameters . In addition, the estimates of  and  are not unique. For each positive and nonzero constant a, we have:

(3)

The constraint  or  can be used to obtain an identifiable solution for  and  (McNicholas and Murphy, 2010; McNicholas and Subedi, 2012; Anderlucci and Viroli, 2015a; Gallaugher and McNicholas, 2017a; Gallaugher and McNicholas, 2017b; Gallaugher and McNicholas, 2019)

2.2 The decomposition of covariance matrices

Restrictions on mixture parameters are typically constructed by constraining covariance matrices. Further, restrictions on mean parameters can be imposed, for example, by considering a linear model of mean parameters instead of the parameters themselves [17], [28]. To achieve parsimonious models, eigenvalue and the modified Cholesky decompositions were used for the between and within covariance matrices, respectively.

2.2.1 The eigenvalue decomposition

Celeux and Govaert (1995), as well as Banfield and Raftery (1993) utilized the eigenvalue decomposition in multivariate normal mixtures. This decomposition was used for the other multivariate mixture distributions such as t-mixture distributions [21], along with skew-normal and skew-t mixture distributions [22] for clustering, classification, and discriminant analysis. On the other hand, Viroli (2011) and. Sarkar et al. (2020) applied the eigenvalue decomposition in the mixture of MVNDs. This parameterization includes the expression within component-covariance matrix () in terms of its eigenvalue decomposition as 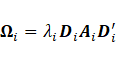, where  denotes the matrix of eigenvectors Furthermore,  is a diagonal matrix whose elements are proportional to the eigenvalues of  and  represents the associated proportionality constant. Different sub-models can be defined by considering homoschedastic or varying quantities across mixture components. According to Fraley and Raftery (2002) and Viroli (2011), the names of eight sub-models are provided in Table 1.

2.2.2 Modified Cholesky decomposition

The between component-covariance matrix () of the multivariate longitudinal data can be decomposed by the modified Cholesky decomposition. McNicholas and Murphy (2010) in addition to McNicholas and Subedi (2012) employed the above-mentioned decomposition in clustering longitudinal data by multivariate normal and t-mixture distributions, respectively. For multivariate longitudinal data, Anderlucci and Viroli, (2015a) used this decomposition, along with the eigenvalue decomposition for the between and within covariance structures in the mixture of MVNDs, respectively. The modified Cholesky decomposition was expressed as 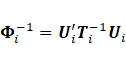 where  is a unique lower triangular matrix with diagonal elements 1 and  denotes a unique diagonal matrix with strictly positive diagonal entries representing innovation variances. The matrix  has the following form:

)4(

The lower diagonal elements in  equal the negative coefficients resulted from the regression of  on  [32]:

)5(

On the other hand, different orders (m) can be considered in matrix , where m can range from 0 to T-1. The lower orders provide more parsimonious models so that m=0 and m=1 equal the independency of different times and the dependency of  on a previous time (), and the like. Accordingly, the modified Cholesky decomposition for the temporal covariance matrix equals the generalized autoregressive with process order m, GAR(m). Thus, the r^th row elements of matrix  which should be estimated can be written as follows:

)6(

Additionally, matrix  can be defended as  (Isotropic) for a more parsimonious model. In addition, different sub-models can be defined by considering homoschedastic or varying quantities (i.e.,  and ) across mixture components. Table 1 presents the names of the four sub-models for the structure of temporal covariance according to the nomenclature of Anderlucci and Viroli (2015a). These names are defined based on the heteroscedastic (GAR) or homoscedastic (EGAR) of  and the isotropic of .

 

Table 1:Parsimonious within and temporal covariance structures, descriptions and number of parameters

	Descriptions	Components			Number of parameters
VVV	Heteroscedastic components
EEV	Ellipsoidal, equal volume and equal space
EEE	Homoscedastic components
III	Spherical components with unit volume
VVI	Diagonal but varying variability components
EEI	Diagonal and homoscedastic components
VII	Spherical components with varying volume
EII	Spherical components without varying volume
GAR(m)	Heteroscedastic components
GARI(m)	GAR + Isotropic for
EGAR(m)	Homoscedastic components
EGARI(m)	EGAR+ Isotropic for

: The number of  parameters

 

3. Method

3.1 Estimation of parameters

To find the maximum likelihood estimators for mixture parameters, the present study used an expectation-maximization (EM) algorithm for the mixture of matrix-variate t-distributions (MVTDs).

Assume that , where n is the number of observations, be a random sample of matrices from the mixture of MVTDs, and  denotes the component membership of observation j. Further,  if the j^th observation is from component i, otherwise, , where  and . Based on the representation of normal-variance mixture, MVTDs are expressed as follows:

(7)

Based on the hierarchical representation of the MVTDs, the complete data log-likelihood  can be written as follows:

(8)

An EM algorithm is as follows:

I.      Initialization: Initialize parameters , , , , and , setting .

II.    E-step: Update , , and , where

 

	(9)
	(10)

 

(11)

where  represents the digamma function. Furthermore, is calculated based on  distribution, which has a gamma distribution with parameters , and  is achieved using the moment-generating function of .

III.              M-step: Update , , , , and . The order of parameter estimation is as follows (1):   and ; (2) ; (3) ; (4)

 

1.      Update  and

(12)

2.      Update  

Assuming that , the  is proportional to  with . The estimates o parameters for the eight sub-models are provided below.

·        Sub-model VVV: The maximization of 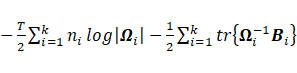 with respect to  leads to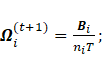

·        Sub-model EEE: The maximization of 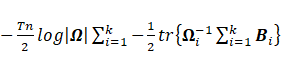, where 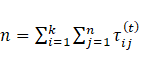, with respect to  leads to  ;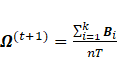

·        Sub-model VVI: The maximization of  with respect to  leads to  and;

·        Sub-model EEI: The maximization of 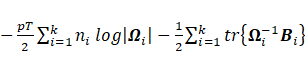 with respect to  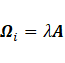leads to 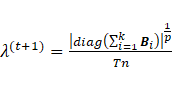and;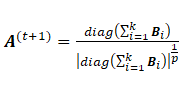

·        Sub-model VII: The maximization of 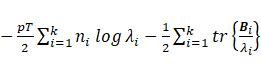 with respect to  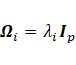leads to ;

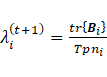·        Sub-model EII: The maximization of 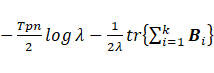 with respect to  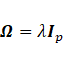leads to ;

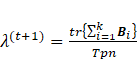·        Sub-model EEV: The maximization of  with respect to  leads to 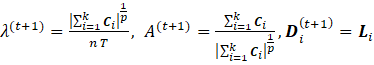, where for  , and  are derived from the eigenvalue decomposition of the symmetric positive definite matrix   with the eigenvalues in the diagonal matrix  in descending order.

·        Sub-model III: This situation equals the independence of the responses thus no parameters are available.

Further estimation details related to the covariance matrix  are provided in (Celeux and Govaert, 1995; Viroli, 2011; L Anderlucci and Viroli, 2015a; Sarkar et al., 2020).

3.      Update

Considering that  is proportional to . The estimates of parameters for the four sub-models are presented as follows:

·        Sub-model GAR(m): The maximization of 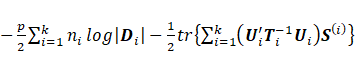 with respect to  leads to the r^th row estimation of matrix  as

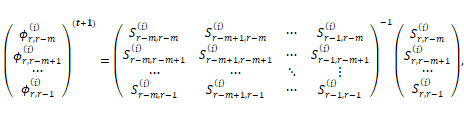
and matrix, where  and  is the l^th-row and r^th-column element of matrix .

·        Sub-model GARI(m): The maximization of  with respect to  leads to the same estimate of  as sub-model GAR(m) and estimate .

·        Sub-model EGAR(m): The maximization of  with respect to  leads to the same estimate of  as sub-model GAR(m) by replacing  instead of  and estimate .

·        Sub-model EGARI(m): The maximization of  with respect to  leads to the same estimate of  as sub-model EGAR(m) and estimate .

Refer to (McNicholas and Murphy, 2010; McNicholas and Subedi, 2012; Anderlucci and Viroli, 2015a) for further details on the estimation of the covariance matrix .

4.      Update

For the degree of freedom, two situations were considered, including equal and unequal  across mixture components (constrained and unconstrained respectively). Given , , , , and , the estimations of  are calculated by finding the root of equations (13) and (14) in constrained and unconstrained situations, respectively.

	(13)
	(14)

IV.   Check the convergence criterion: If not satisfied, set  and go to step II of the EM algorithm iteration.

3.2 Model selection and convergence criterion

It is possible to define a large family () of possible mixture models by allowing different sub-models for covariance matrices  and  with different orders for matrix , , 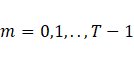and constrained/unconstrained for . The model can be selected according to the Bayesian information criterion (BIC) as follows [33]:

)15(

where  and  indicate the maximized log-likelihood and the maximum likelihood estimate of , respectively. Additionally,  and n are the number of free parameters in the model and the number of observations, respectively.

Other criteria are employed in addition to BIC to estimate the number of mixture components, such as Integrated Completed Likelihood (ICL), which is computed as follows [34]:

)16(

where MAP (τ_ij^(t)) )=1 if the max_i=1,…,k {τ_ij^{(t)}=i, otherwise, MAP(τ_ij(t))=0, j=1 ,…,n and i=1,…,k.}

In general, 20 random multistate points were considered given that the starting values of the EM algorithm could affect the estimated parameters. If the convergence criterion  is met, the EM algorithm is stopped, and the range of values for  is limited to between 2 and 200 [21]. These models have been written in R and are accessible on request.

3.3 Calculate the standard error of parameters

The observed information matrix may be used to calculate the parameter's standard error. The observed information matrix is computed as , where  is the Hessian matrix of the likelihood function for observation j. The hessian function in numDeriv package in R software could be used to calculate  (Anderlucci and Viroli, 2015a).

4. Simulation studies and real data

4.1 Simulation 1

The first simulation study was conducted to evaluate the ability of the algorithm for recognizing the temporal structure. The features of simulation study 1 were: a number k of mixture components equal to 3, a k-vector of the degrees of freedom equal to 5, 5, 5, and a 4  4 within covariance matrix  with a structure equals to VVV. In addition, other features included a 66 temporal covariance matrix  with a structure equals to GAR(1) and GAR(3), and a sample size n equals 100, 200, 500, and 1000. For each setting, 100 datasets were generated from the mixture of the MVTDs based on the defined within and temporal covariance matrices. Then, the mixture of MVTDs and MVNDs was run for five different models according to different orders for : GAR(1), GAR(2), GAR(3), GAR(4), and GAR(5). The best model was chosen according to the BIC and ICL. Table 2 contains the number of times a model with GAR(1) and GAR(3) structures for  was selected as the best model based on the BIC and ICL. To converge the EM algorithm, MVTD models with the constrained degrees of freedom were fitted in settings with the GAR(3) true structure and the sample sizes of 100 and 200 while MVTD models with unconstrained degrees of freedom were run in other settings.

The percentage (number) of correct model selection with MVTD is equal to 100 in all cases, and it ranges from 97 to 100 for MVNDs. In a situation with a true model GAR(3), this percentage varied from 99 to 100 and 93 to 99 for MVTD and MVND, respectively.

Table 2: The number of times a model with GAR(1) or GAR(3) structure for  was chosen according to the BIC and ICL criterion, from the simulation 1

n
		GAR(1)		GAR(2)	GAR(3)	GAR(4)	GAR(5)
	Model		True Sub-model: GAR(1)
100	MVTD	100		0	0	0	0
	MVND	97		3	0	0	0
200	MVTD	100		0	0	0	0
	MVND	99		1	0	0	0
500	MVTD	100		0	0	0	0
	MVND	100		0	0	0	0
1000	MVTD	100		0	0	0	0
	MVND	99		1	0	0	0
			True Sub-model: GAR(3)
100	MVTD	0		0	97	2	1
	MVND	1		0	93	4	2
200	MVTD	0		0	100	0	0
	MVND	0		1	95	3	1
500	MVTD	0		0	100	0	0
	MVND	0		0	98	1	1
1000	MVTD	0		0	100	0	0
	MVND	0		0	99	1	0

 

4.2 Simulation 2

It is known that t-distributions can recover normal distributions by estimating larger values of the degrees of freedom parameters. Further, t-distribution mixture models can be used when mixture components are derived from normal and t-distributions. The simulation study 2 was performed to evaluate the ability of MVTDs to recover the MVNDs in multivariate longitudinal data. To this end, datasets were generated from two-component (k=2), matrix-variate mixture models. The MVND and MVTD were the first and second components, respectively, and the same covariance structures with different parameter values were used accordingly. Other features (i.e., , , and sample size) in this simulation are similar to the first simulation study. For each setting, 100 datasets were generated from mixture distributions based on the defined within and temporal covariance matrices. Further, the mixture of MVTDs and MVNDs was run for five different models of GAR(1), GAR(2), GAR(3), GAR(4), and GAR(5). Table 3 presents the average values of the degree of freedom (standard deviation) of a model with GAR(1) and GAR(3) structures for . Based on the obtained data, the sample size of 100 was not considered for a setting with the GAR(3) true temporal due to the lack of convergence of the EM algorithm. Given k (=2) and  (VVV), the estimated degrees of freedom demonstrated that the first component was normal. Furthermore, the degrees of freedom estimates were computed to be close to true values in MVTD mixture models.

Based on Tables 3 and 5, the true model GAR(3) had a worse performance compared to the true model GAR(1). Therefore, the results related to the simulation studies of the true model GAR(3) are presented in the continuation.

Additionally, the misclassification error rate (MISC) and the measure of accuracy () for mean and covariance matrices were computed for each dataset and model in order to compare the two models in parameter estimates. Therefore, the accuracy measures of ,  (=VVV), , and  (=GAR) were calculated by the following expressions (Anderlucci and Viroli, 2015b):

)17(

where the lower accuracy measure () implies higher accuracy for parameters.

Table 4 provides the average (standard deviation) values of MISC and the accuracy measures of a model with GAR(3) for . Considering k (=2) and  (VVV), the accuracy measures (, , and ) were not sensitive to the misspecification of the order of the temporal covariance (m=1, 2, …, 5), and these values were nearly identical in MVTD and MVND mixture models. However, the values of the accuracy measure () relied on the misspecification of the temporal covariance order. In the two models, the accuracy measure ) of the lower orders () was larger compared to the higher orders (). It should be noted that MVND mixture models tend to overestimate the accuracy measure () compared to MVTD mixture models. Eventually, the accuracy measures in both models decreased by an increase in the sample size. The mean compute time for fitting the mixture of MVTDs vs as MVNDs with the true model GAR(3) was 6.66 vs. 0.37 for n=100, 10.17 vs. 0.62 for n=200, 23.44 vs. 1.30 for n=500, and 46.86 vs 2.59 for n=1000.

Table 3: Mean (S.D) of degree of freedom with GAR(1) or GAR(3) structure for from simulation 2

n
	GAR(1)	GAR(2)	GAR(3)	GAR(4)	GAR(5)
	True Sub-model: GAR(1)
100	174.9 (48.2)	175.6 (46.5)	176.3 (45.6)	176.7 (45.2)	177.4 (45.6)
	5.42 (1.30)	5.42 (1.32)	5.43 (1.31)	5.43 (1.30)	5.43 (1.30)
200	189.4 (30.1)	189.3 (30.4)	189.8 (29.6)	189.9 (29.5)	190.2 (29.2)
	5.09 (0.79)	5.09 (0.79)	5.09 (0.79)	5.10 (0.79)	5.10 (0.78)
500	192.0 (23.3)	191.9 (23.2)	192.4 (22.7)	192.6 (22.4)	192.6 (22.3)
	5.05 (0.51)	5.05 (0.51)	5.05 (0.51)	5.05 (0.51)	5.05 (0.51)
1000	199.6 (3.9)	199.6 (3.7)	199.7 (3.3)	199.7 (2.9)	199.7 (2.6)
	4.99 (0.35)	4.99 (0.35)	4.99 (0.35)	4.99 (0.35)	4.99 (0.35)
	True Sub-model: GAR(3)
200	175.8 (48.6)	160.8 (31.5)	189.3 (31.2)	189.7 (30.8)	189.9 (30.4)
	4.75 (0.84)	4.77 (0.85)	5.09 (0.87)	5.10(0.88)	5.10 (0.88)
500	116.2 (44.3)	167.1 (42.9)	195.0 (19.7)	195.1(19.6)	195.1 (19.6)
	4.74 (0.43)	4.85 (0.43)	5.06 (0.43)	5.07(0.43)	5.07 (0.43)
1000	119.6 (41.9)	178.7 (34.2)	198.2 (9.3)	198.2(9.2)	198.2 (9.2)
	4.70 (0.38)	4.97 (0.39)	5.05 (0.41)	5.05(0.41)	5.05 (0.41)

 

Table 4: Mean (S.D) of MISC and accuracy measures with GAR(3) structure for from simulation 2

		Model
n			GAR(1)	GAR(2)	GAR(3)	GAR(4)	GAR(5)
200	MISC	MVTD	0	0	0	0	0
		MVND	0.0001(0.001)	0.0001(0.001)	0.0001(0.001)	0.0001(0.001)	0.0001(0.001)
		MVTD	0.09 (0.01)	0.09 (0.01)	0.09 (0.01)	0.09 (0.01)	0.09 (0.01)
		MVND	0.10 (0.01)	0.10 (0.01)	0.10 (0.01)	0.10 (0.01)	0.10 (0.01)
		MVTD	0.23 (0.002)	0.23 (0.001)	0.23 (0.001)	0.23 (0.001)	0.23 (0.001)
		MVND	0.23 (0.003)	0.23 (0.002)	0.23 (0.001)	0.23 (0.001)	0.23 (0.001)
		MVTD	0.49 (0.02)	0.44 (0.02)	0.40 (0.02)	0.40 (0.02)	0.40 (0.02)
		MVND	0.57 (0.06)	0.52 (0.13)	0.48 (0.14)	0.48 (0.14)	0.48 (0.14)
		MVTD	0.33 (0.002)	0.20 (0.01)	0.10 (0.02)	0.15 (0.04)	0.18 (0.04)
		MVND	0.33 (0.002)	0.20 (0.02)	0.11 (0.03)	0.17 (0.05)	0.21 (0.06)
500	MISC	MVTD	0	0	0	0	0
		MVND	0	0	0	0	0
		MVTD	0.08 (0.01)	0.08 (0.01)	0.08 (0.01)	0.08 (0.01)	0.08 (0.01)
		MVND	0.09 (0.01)	0.09 (0.01)	0.09 (0.01)	0.09 (0.01)	0.09 (0.01)
		MVTD	0.18 (0.0003)	0.18 (0.0002)	0.18 (0.0002)	0.18 (0.0002)	0.18 (0.0002)
		MVND	0.18 (0.0003)	0.18 (0.0003)	0.18 (0.0003)	0.18 (0.0003)	0.18 (0.0003)
		MVTD	0.47 (0.01)	0.38 (0.01)	0.35 (0.01)	0.35 (0.01)	0.35 (0.01)
		MVND	0.51 (0.02)	0.45 (0.02)	0.41 (0.02)	0.41 (0.02)	0.41 (0.02)
		MVTD	0.30 (0.002)	0.19 (0.004)	0.08 (0.01)	0.08 (0.01)	0.08 (0.01)
		MVND	0.30 (0.003)	0.19 (0.004)	0.09 (0.01)	0.09 (0.01)	0.09 (0.01)
1000	MISC	MVTD	0	0	0	0	0
		MVND	0	0	0	0	0
		MVTD	0.06 (0.01)	0.06 (0.01)	0.06 (0.01)	0.06 (0.01)	0.06 (0.01)
		MVND	0.07 (0.01)	0.07 (0.01)	0.07 (0.01)	0.07 (0.01)	0.07 (0.01)
		MVTD	0.15 (0.0002)	0.15 (0.0002)	0.15 (0.0002)	0.15 (0.0002)	0.15 (0.0002)
		MVND	0.15 (0.0002)	0.15 (0.0002)	0.15 (0.0002)	0.15 (0.0002)	0.15 (0.0002)
		MVTD	0.31 (0.01)	0.27 (0.01)	0.27 (0.01)	0.27 (0.01)	0.27 (0.01)
		MVND	0.42 (0.03)	0.40 (0.02)	0.37 (0.02)	0.37 (0.02)	0.37 (0.02)
		MVTD	0.28 (0.001)	0.17 (0.001)	0.05 (0.001)	0.05 (0.001)	0.05 (0.001)
		MVND	0.28 (0.001)	0.20 (0.001)	0.06 (0.01)	0.06 (0.01)	0.06 (0.01)

 

4.3 Simulation 3

The number of components was considered constant and the mixture models were fitted in the two preceding simulation studies. In the third simulation study, the ability of MVTD and the MVND mixture models was evaluated regarding recognizing the true number of mixture components when the data were generated from MVTD mixture models. Then, the impact of the misspecification of the temporal matrix on the estimation of the number of components was investigated as well. The same parameters were used in this simulation as in the first simulation.

For each setting, 100 datasets were generated from the model with a GAR(3) structure. In addition, a different number of mixture components (k = 2, 3, and 4) was considered to evaluate the choice of k. Table 5 presents the number of times a model with a particular number of mixture components was chosen as the best model in each of the five different models of GAR(1), GAR(2), GAR(3), GAR(4), and GAR(5). Approximately the correct number of components (k=3) was selected for MVTDs in all cases. However, MVNDs tend to overestimate (k=4) the number of true components. As the sample size increased, the correct number of components reached 100 in MVTD, while it was completely overestimated in MVND. Also, in a small sample size (n=200), the ability to detect the correct number of components increased with the increase of m in both models.

Table 5: The number of times a model with the true number of component (k=3) and GAR(3) structure for  for the different temporal structures was chosen from simulation 3

n	Model	k	True Sub-model: GAR(3)
			GAR(1)	GAR(2)	GAR(3)	GAR(4)	GAR(5)
200	MVTD	2	0	0	0	0	0
		3	95	99	96	100	100
		4	5	1	4	0	0
	MVND	2	0	0	0	0	0
		3	42	53	62	68	73
		4	58	47	38	32	27
500	MVTD	2	0	0	0	0	0
		3	100	100	100	100	100
		4	0	0	0	0	0
	MVND	2	0	0	0	0	0
		3	0	0	0	0	0
		4	100	100	100	100	100
1000	MVTD	2	0	0	0	0	0
		3	100	100	100	100	100
		4	0	0	0	0	0
	MVND	2	0	0	0	0	0
		3	0	0	0	0	0
		4	100	100	100	100	100

 

4.4 Real data: Gastrointestinal (GI) cancers

The age-standardized death rates of the three most common GI cancers were extracted from the Our World In Data website [36]. The information included the death rates (per 100,000 populations) of colon and rectum, stomach, and liver cancers in 186 countries during 1990-2015 (at 5-year intervals), is a matrix with dimension . A mixture of MVTDs and MVNDs was fitted with k ranging from 1 to 10. The best sub-model based on the BIC and ICL is (GAR(2), VVV) with k=7 in the mixture of MVNDs and (GAR(4), VVV) with the constrained degrees of freedom and k=6 in the mixture of MVTDs (Table 6). The estimated degree of freedom for the mixture of the MVTDs was . Further, stomach and liver cancer death rates in some countries were extremely higher compared to other countries. Thus, the mixture of the MVND model provided an additional cluster to allow outliers.

Table 6: Results of the mixture of the MVTD and MVND models for the three common GI cancers

Model	BIC	ICL			m	k		RMSD	Compute time for fitting (Second)
MVTD	9275.63	9240.58	VVV	GAR	4	6	3.33	9.42	165.42
MVND	9666.63	9683.78	VVV	GAR	2	7	-	11.20	127.80

 

Table 7: Estimated component means of the countries based on the death rates of the three common GI cancers resulted from the mixture of the MVTD models

 

We also fitted a finite mixture of skew matrix-variate distributions introduced by Gallaugher and McNicholas (2017b) to GI data. These matrix-variate distributions are skew-t, generalized hyperbolic, variance-gamma, and normal inverse Gaussian distributions that we did not consider eigenvalue and the modified Cholesky decompositions for the between and within covariance matrices for those, respectively. Because of the huge number of parameters, any of these finite mixture had not been converge. Given k, the number of parameters in these skew matrix-variates is 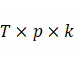 to greater than the matrix-varieties distributions.

The root mean square deviation (RMSD), the quadratic mean of the differences between the observed values and predicted values, values for the mixture of MVNDs and MVTDs were 11.20 and 9.42, respectively (Table 6). For more details, maps of the included countries in each cluster of MVTD and MVND models are presented in Figures 1 and 2, respectively. The estimated component mean for each cluster of MVTD models is shown in Table 7. The colon and rectum, liver, and stomach cancer death rates were growing, nearly stable, and decreasing in the first cluster countries, respectively. The behaviour of the countries in the second and third clusters was similar to the first cluster, with the exception that the rate of decrease in liver cancer in the second cluster was slower, and the rate in the third cluster was between the first and second clusters. The fourth cluster countries' patterns are identical to the second cluster, although the decline in the liver is quicker. The colon and rectum and liver are growing in fifth cluster countries, whereas the stomach is dropping (with the highest rate of decrease among the clusters). Countries in the sixth cluster behaved similarly to those in the fifth, with the exception that the rate of change in the colon and rectum was quicker. According to Figure 2, the second cluster countries, which mostly include African and Arab countries, have the lowest death rates in the three cancers.

 

 

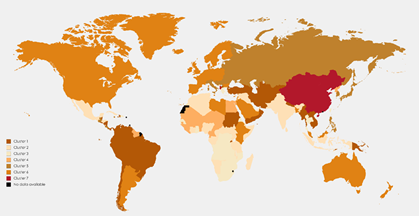
Figure 1: Map of clustering countries based on the death rates of the three common GI cancer resulted from the mixture of the MVNDs

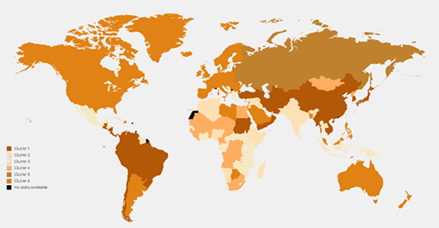
Figure 2: Map of clustering countries based on the death rates of the three common GI cancer resulted from the mixture of the MVTDs

 

5. Conclusion

In the present study, a family of finite matrix-variate t-distributions was evaluated for clustering multivariate longitudinal datasets. To this end, two types of constraints were utilized for covariance structures, including the eigenvalue and modified Cholesky decompositions for the within and temporal covariance matrices, respectively.

Based on accuracy measures () in the mixture models of MVTD and the MVND, no differences were observed between the estimation of , , and  matrices under different orders of temporal covariance structures in each model in simulation studies. Further, these values were similar in both models. On the other hand, the estimation of matrix  relies on the misspecification of . Thus, the accuracy measure s should have the least value compared to lower orders if the order of the incorrect temporal structure is equal to or greater than the correct order of the temporal structure. The estimations of matrix T and the number of mixture components k are overestimated in MVND models if the datasets have a heavy-tail or outlier observations. These properties were demonstrated by McNicholas and Subedi (2012) in the clustering of longitudinal data using the mixture of multivariate t-distributions. On the other hand, the time it took to fit a mixture of MVTDs was much longer than it required to fit a mixture of MVNDs, which is a trade-off for more precision.

The mixture of MVTDs commonly selected the model with the right temporal structure and the right number of mixture components. Based on the MISC and accuracy measures, a perfect separation was found between the mixture components and the good accuracy of parameter estimation in this mixture model. The results of these simulation studies regarding evaluating different abilities of the finite mixtures of MVTDs were similar to those of simulations in the finite mixture of the MVNDs (Anderlucci and Viroli, 2015b).

The age-standardized death rates of the three most common GI cancers (i.e., colon and rectum, stomach, and liver) from 186 countries were clustered between 1990 and 2015 (a 5-year interval) using the mixture of MVTD and MVND models. Based on the BIC and ICL, the same within and temporal covariance structures were selected in both models although the order of the temporal structure was higher in the MVTD mixture. On the other hand, one more component was available in the MVTD mixture for including outlier death rates. Based on the BIC and ICL and RMSD, MVTD mixture models better fitted to the clustering death rates of the three common GI cancers of the countries compared to MVND mixture models.

Finally, the large value of the RMSD revealed that other matrix-variate distributions (i.e., asymmetric matrix-variate distributions) could be appropriate in this regard. In our future work, we will consider the parsimonious covariance of the finite mixture of skewed matrix-variate distributions for the clustering three-way data.

 

References

[1]        G. J. McLachlan and D. Peel, Finite mixture models. New York (NY): John Wiley & Sons, 2000. View Article

[2]        P. D. McNicholas, Mixture model-based classification, 1st ed. Chapman & Hall/CRC, 2016. View Article

[3]        D. Peel and G. J. McLachlan, “Robust mixture modelling using the t distribution,” Stat. Comput., vol. 10, no. 4, pp. 339–348, 2000. View Article

[4]        T. I. Lin, “Maximum likelihood estimation for multivariate skew normal mixture models,” J. Multivar. Anal., vol. 100, no. 2, pp. 257–265, Feb. 2009. View Article

[5]        T. I. Lin, “Robust mixture modeling using multivariate skew t distributions,” Stat. Comput., vol. 20, no. 3, pp. 343–356, Jul. 2010. View Article

[6]        A. O’Hagan, T. B. Murphy, I. C. Gormley, P. D. McNicholas, and D. Karlis, “Clustering with the multivariate normal inverse Gaussian distribution,” Comput. Stat. Data Anal., vol. 93, pp. 18–30, Jan. 2016. View Article

[7]        R. P. Browne and P. D. McNicholas, “A mixture of generalized hyperbolic distributions,” Can. J. Stat., vol. 43, no. 2, pp. 176–198, Jun. 2015. View Article

[8]        U. J. Dang, R. P. Browne, and P. D. McNicholas, “Mixtures of multivariate power exponential distributions,” Biometrics, vol. 71, no. 4, pp. 1081–1089, Dec. 2015. View Article

[9]        A. K. Gupta and D. K. Nagar, Matrix Variate Distributions, 1st ed. New York: Chapman and Hall/CRC, 2000.

[10]     C. Viroli, “Finite mixtures of matrix normal distributions for classifying three-way data,” Stat. Comput., vol. 21, no. 4, pp. 511–522, Oct. 2011. View Article

[11]     L. Anderlucci and C. Viroli, “Covariance pattern mixture models for the analysis of multivariate heterogeneous longitudinal data,” Ann. Appl. Stat., vol. 9, no. 2, pp. 777–800, 2015. View Article

[12]     F. Z. Doğru, Y. M. Bulut, and O. Arslan, “Finite mixtures of matrix variate t distributions,” Gazi Univ. J. Sci., vol. 29, no. 2, pp. 335–341, Jun. 2016.

[13]     M. P. B. Gallaugher and P. D. McNicholas, “A matrix variate skew- t distribution,” Stat, vol. 6, no. 1, pp. 160–170, 2017. View Article

[14]     M. P. B. Gallaugher and P. D. McNicholas, “Three skewed matrix variate distributions,” Stat. Probab. Lett., vol. 145, pp. 103–109, Feb. 2019. View Article

[15]     M. P. B. Gallaugher and P. D. McNicholas, “Finite Mixtures of Skewed Matrix Variate Distributions,” Mar. 2017. View Article

[16]     P. D. McNicholas and T. B. Murphy, “Model-based clustering of longitudinal data,” Can. J. Stat., vol. 38, no. 1, pp. 153–168, 2010. View Article

[17]     P. D. McNicholas and S. Subedi, “Clustering gene expression time course data using mixtures of multivariate t-distributions,” J. Stat. Plan. Inference, vol. 142, no. 5, pp. 1114–1127, May 2012. View Article

[18]     J. D. Banfield and A. E. Raftery, “Model-Based Gaussian and Non-Gaussian Clustering,” Biometrics, vol. 49, no. 3, pp. 803–821, Sep. 1993. View Article

[19]     G. Celeux and G. Govaert, “Gaussian parsimonious clustering models,” Pattern Recognit., vol. 28, no. 5, pp. 781–93, 1995. View Article

[20]     C. Fraley and A. E. Raftery, “Model-Based Clustering, Discriminant Analysis, and Density Estimation,” J. Am. Stat. Assoc., vol. 97, no. 458, pp. 611–631, Jun. 2002. View Article

[21]     J. L. Andrews and P. D. McNicholas, “Model-based clustering, classification, and discriminant analysis via mixtures of multivariate t-distributions,” Stat. Comput., vol. 22, no. 5, pp. 1021–1029, 2012. View Article

[22]     I. Vrbik and P. D. McNicholas, “Parsimonious skew mixture models for model-based clustering and classification,” Comput. Stat. Data Anal., vol. 71, pp. 196–210, Mar. 2014. View Article

[23]     L. Anderlucci and C. Viroli, “Covariance pattern mixture models for the analysis of multivariate heterogeneous longitudinal data,” Ann. Appl. Stat., 2015. View Article

[24]     S. Sarkar, X. Zhu, V. Melnykov, and S. Ingrassia, “On parsimonious models for modeling matrix data,” Comput. Stat. Data Anal., vol. 142, p. 106822, Feb. 2020. View Article

[25]     C. Viroli, “Finite mixtures of matrix normal distributions for classifying three-way data,” Stat. Comput., vol. 21, no. 4, pp. 511–522, Oct. 2011. View Article

[26]     S. D. Tomarchio, “On Parsimonious Modelling via Matrix-Variate t Mixtures,” in Classification and Data Science in the Digital Age, Springer International Publishing, 2023, pp. 393–401. View Article

[27]     A. K. Gupta, T. Varga, and T. Bodnar, Elliptically Contoured Models in Statistics and Portfolio Theory, 2nd ed. New York: Springer, 2013. View Article

[28]     G. Z. Thompson, R. Maitra, W. Q. Meeker, and A. Bastawros, “Classification with the matrix-variate-t distribution,” J. Comput. Graph. Stat., vol. 29, no. 3, pp. 668–74, Jul. 2020. View Article

[29]     G. Celeux and G. Govaert, “Gaussian parsimonious clustering models,” Pattern Recognit., vol. 28, no. 5, pp. 781–793, May 1995. View Article

[30]     J. D. Banfield and A. E. Raftery, “Model-Based Gaussian and Non-Gaussian Clustering,” Biometrics, vol. 49, no. 3, pp. 803–821, Sep. 1993. View Article

[31]     C. Fraley and A. E. Raftery, “Model-Based Clustering, Discriminant Analysis, and Density Estimation.,” J. Am. Stat. Assoc., vol. 97, no. 458, pp. 611–631, Jun. 2002. View Article

[32]     M. Pourahmadi, “Joint mean-covariance models with applications to longitudinal data: unconstrained parameterisation,” Biometrika, vol. 86, no. 3, pp. 677–690, Sep. 1999. View Article

[33]     G. Schwarz, “Estimating the Dimension of a Model,” Ann. Stat., vol. 6, no. 2, pp. 461–464, Mar. 1978. View Article

[34]     I. C. Gormley, T. B. Murphy, and A. E. Raftery, “Model-Based Clustering,” Annu. Rev. Stat. Its Appl., vol. 10, no. 1, pp. 573–595, Mar. 2023. View Article

[35]     L. Anderlucci and C. Viroli, “Supplement to “Covariance pattern mixture models for the analysis of multivariate heterogeneous longitudinal data,” 2015. View Article

[36]     M. Roser and H. Ritchie, “Cancer,” Our World in Data, 2019. [Online]. Available: [Accessed: 16-Sep-2019]. View Article