Journal of Machine Intelligence and Data Science (JMIDS)

1. Introduction

The governor of the PSH plants has the primary function of controlling the rotational speed of the turbine by adjusting the turbine’s gate to regulate the water flow through it. The proportional, integral, and derivative (PID) controllers have been widely known and utilized in many industrial control processes because of their simplicity and maturity, therefore adopted mostly in PSH governors [1]. Notwithstanding their popularity, PID controllers have constraints such as their restriction to only single-input single-output (SISO) applications and their inability to optimally control complex systems that change over time, therefore requiring their parameters to be tuned and retuned as the system changes [1], [2].

In some cases, the PID controller tuning methods used do not always yield the optimal parameters, in turn, leading to a decrease in the efficiency of the system [3]. To help address this concern, several control approaches, such as adaptive control and intelligent systems such as Fuzzy Logic and Artificial Neural Networks have been proposed and studied in several research papers.

Reinforcement learning (RL) involves an agent training its policy to optimally map a given state to an action to maximize the total accumulated reward. Recently, by combining it with deep neural networks to approximate its action-value function, it has been used to solve complex tasks with high dimensions such as in robotics, and also to achieve human-level performance on many Atari games [4], [5]. These evolutions bring new ideas on how to control complex control tasks due to their powerful flexibility in changing and uncertain environments [6].

The use of RL algorithms has been proposed in some power system sectors. In [7], a DDPG agent was employed to update the controller parameters in the adaptive control of the static synchronous compensator with additional damping controller (STATCOM-ADC). In [8], deep Q networks (DQN) was adopted to optimally self-tune the parameters of a hydro-governor PID controller to achieve better performance in preventing ultra-low frequency oscillation. Unlike in [7] and [8], Huang et al. in [6] achieved an improvement of 21.8% in cumulative bus voltage deviation per month by employing a deep deterministic policy gradient (DDPG) agent to control the active and reactive power of a PSH on a pumped storage hydro-wind-solar system.

Unlike in [8], where DQN was employed to tune the parameters of the hydro-governor PID controller, this work proposes to utilize a DDPG-based agent in place of the PID controller to control the gate of the turbine as its dynamics change due to the change in head. The DDPG was employed because of its ability to handle a high-dimensional continuous state-action space.

The rest of this paper is arranged as follows. Section 2 presents the system setup. Section 3 presents the proposed DDPG-based agent and the modeling of the hydraulic system. Finally, sections 4 and 5 respectively present simulation results, and draws conclusions.

2. System Setup

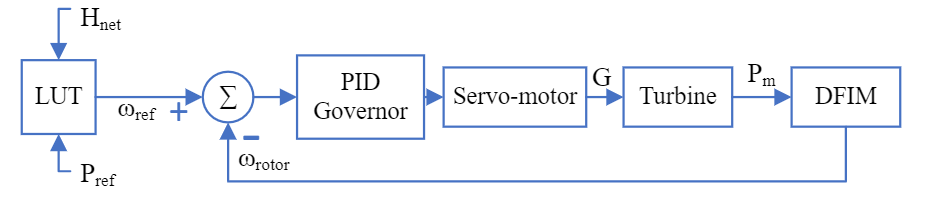
For this study, an adjustable speed pumped storage hydropower (AS-PSH) that utilizes a doubly-fed induction machine (DFIM) is adopted. Figure 1 shows the generic block diagram of components in a PSH plant setup and its control. The PID governor regulates the turbine speed by controlling the gate G of the turbine through the servomotor. The reference speed tracked by the PID governor is obtained from a look-up table (LUT) using the net head and reference power.

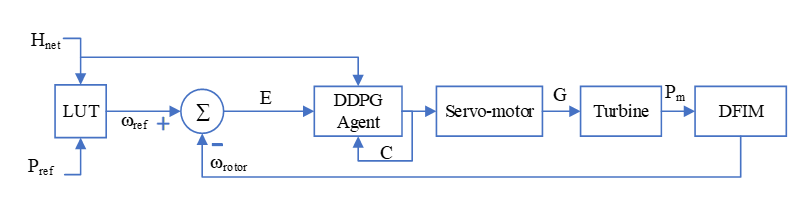
Figure 2 shows the proposed system setup for this work, with the PID governor replaced with a DDPG-based Agent. The inputs to the agent are the available net head, Hnet a vector of the previous controller output, C, and a vector of the error, its derivative, its integral, and their previous values, E.

3. System Component Modeling and Control

Dynamic models of the above components were designed using MATLAB/SIMULINK. As our focus is not on the machine side of this setup, the equivalent circuit model of the DFIM used is not shown here. But can be found in [9], [10].

3. 1. Hydraulic System Modeling

The modeling of the penstock and turbine was done by assuming that we have a rigid conduit and an incompressible fluid. The mechanical power, P_m generated by the turbine is then given as a function of the turbine power coefficient, A_t, the head at the turbines admission, h, the flow, q, the no-load flow, q_nl, the damping coefficient, D, the gate, G, and the deviation in speed, ∆ω, as shown in Eq. 1.

(1)

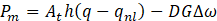
The rate of change of flow in the conduit and the head at the turbine's admission are respectively presented in Eq. 2 and Eq. 3:

(2)

(3)

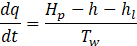
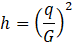
Where H_p represents the head at the penstock entrance, h_l represents the head loss, and T_w represents the water time constant.

3. 2. Servomotor Modelling

The servomotor was modeled as a first-order system as shown in Figure 3, with a gain, K_a and time constant, T_a. A min and max limit were applied to its output for both the gate opening and gate speed.

3. 3. Proposed Deep Deterministic Policy Gradient (DDPG)-based Agent for the Governor

The standard RL setup as shown in Figure 4 consists of an agent that receives an observation x_t from an environment E, takes an action a_t defined by its policy, receives a scalar reward r_t, and updates its policy according to the RL algorithm adopted. To apply RL to a problem, it must be established as a Markov decision process (MDP) which assumes that the next state is only dependent on the current state and action [11].

The MDP is a 4-tuple 〈S,A,P,R〉.

• S is the set of states of the environment. For this study, it is the available net head, the previous controller output, and the deviation of the rotor speed from the reference speed, its derivative and integral, and their previous values.
• A is the set of actions. For this study, it is the control signal to be sent to the servomotor that opens and closes the gate.
• P is the probability P(s_t+1 |s_t,a_t) of the current state, s_t, transitioning to the next state, s_t+1, by executing the action a_t.
• R is the immediate reward r(s_t,a_t ) returned by the environment after executing the action, a_t, and transitioning from s_t to s_t+1. As a speed-tracking problem, this work utilizes the objective function presented in Eq. 4 as its reward function, where e is the deviation of the rotor speed from the reference speed.

(4)

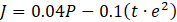
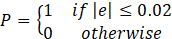
In general, the goal of an MDP is to find a policy π that will maximize a cumulative function of the expected rewards from the kick-off state [12]. In RL, such a function is called the Q-value function shown below in Eq. 5, which describes the expected reward for taking action a_t in state s_t and following policy π afterward:

(5)

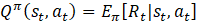
where R_t is the sum of discounted future rewards with a discount factor γ∈[0,1],

(6)

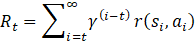
We transform (5) into the Bellman expectation equation as shown in Eq. 7, which relates the value of a state to the expected value of its successor states.

(7)

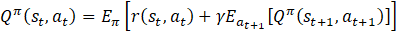
The DDPG as shown in Figure 5 utilizes an actor-critic architecture represented by deep neural networks to solve the MDP and learn the optimal policy, π. The critic network, Q, with parameters, θ^Q, takes state-action pairs (s_t,a_t ) as input to approximate the current Q-value function Q(s_t,a_t|θ^Q). According to [13], its accuracy is improved by updating its parameters θ^Q to minimize the loss function shown in Eq. 8:

(8)

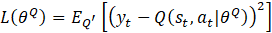
where

(9)

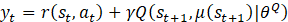
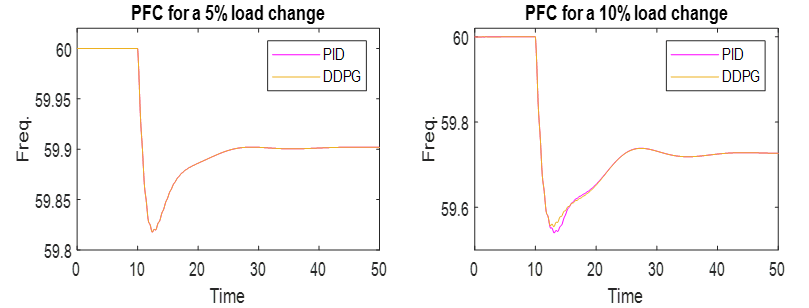
For the actor network μ, it takes the state s_t as input and approximates the policy, π, for selecting the current action, a_t, which interacts with the environment to generate the next state and reward value. According to [14], to ensure that the actor network produces actions that maximize the estimated Q value, its parameters, θ^μ, are updated by the policy gradient theorem shown in Eq. 10.

(10)

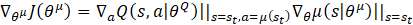
A second set of the actor-critic network is employed by the DDPG algorithm to make the training process stable [15]. This second set of the actor-critic network is called the target with parameters, θ^μ' and θ^Q' for its actor network and critic network, respectively. These parameters are close to that of the main actor-critic network but with a time delay. They are updated by a soft update process as shown below in Eq. 11:

(11)

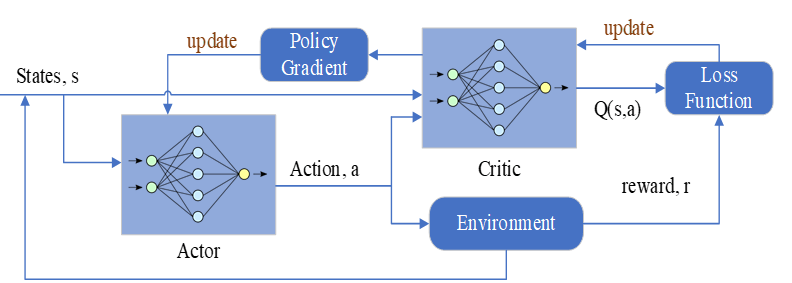
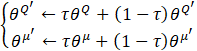
An experience replay buffer D=(e₁,e₂,…,e_M ) of M-size is used to store experience, e=(s_t,a_t,r_t,s_t+1 ) , for each step. This is similar to the human brain storing memory in registers. New experiences overwrite older ones when the buffer capacity is reached. Only N-size mini-batch of experience is selected from D for the gradient calculation and network parameter update. Therefore, (8) can be adjusted to

(12)

(13)

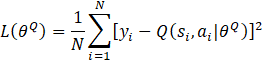
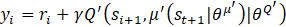
where y_i is the Q-value obtained from the sum of the current reward and the discounted future reward calculated by the target critic network. The main critic network is now updated as shown in Eq. 14,

(14)

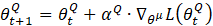
where, α^Q is the learning rate for the critic network. From (12) and (10), we can update the main actor network as shown below:

(15)

(16)

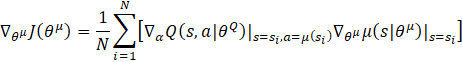
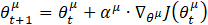
3. 4. Training Process for the Agent

The algorithm used to implement the DDPG agent for the PSH governor controller is shown in Table 1.

As a temporal dynamic system, the data from the ASPSH model is sequential and requires the use of a recurrent neural network (RNN) to better capture its dynamics. Since the use of RNNs appeared to be computationally intensive for this project, a feed-forward neural network (FFNN) is used instead. To account for the temporal dynamics of the system, limited past information of the controller output, the deviation of the rotor speed from the reference speed, its derivative, and its integral were also included as input to the network.

To train the agent, MATLAB and SIMULINK were utilized to execute the above algorithm and also to set up the ASPSH model discussed above as the environment. The training was done for 1000 episodes. For each episode, the environment is run for 100 seconds, and the net available head is issued randomly and maintained throughout the episode, while a random optimal speed reference is issued at a random time in the episode. The hyperparameters utilized for training are shown in Table 2.

4. Results and Discussion

To test the performance of our trained agent as the governor for the ASPSH unit, it was tested for various step changes in power reference at various available net head in the reservoir. Its performance was in turn compared to that of a particle swarm optimized (PSO) PID governor for the same operating condition as shown in Figure 6. For an available net head of 1.00 and 0.98 p.u, a power reference of [0.70 0.74 0.80 0.70] p.u was applied to the system at times [0 120 240 360]s. While, for an available net head of 0.93 and 0.90 p.u, a power reference of [0.62 0.70 0.60 0.65] p.u was applied to the system at times [0 120 240 360]s. The speed references obtained from the LUT are [1.0286 1.0514 1.0857 1.0286] p.u, [1.0250 1.0504 1.0800 1.0280] p.u, [0.9828 1.0286 0.9714 1.0000] p.u, and [0.9828 1.0280 0.9692 1.0000] p.u respectively. From the comparison of the control performance of the DDPG and PID governor presented in Figure 6, the proposed DDPG governor in most cases achieved lesser maximum overshoot and settling time when compared to the PID governor. Because the DFIM of the AS-PSH has its converter control highly involved in controlling the electrical power output of the unit, the focus of this work was on demonstrating the ability of the trained agent to have the turbine follow and track the optimal speed reference required to generate the required electrical power output.

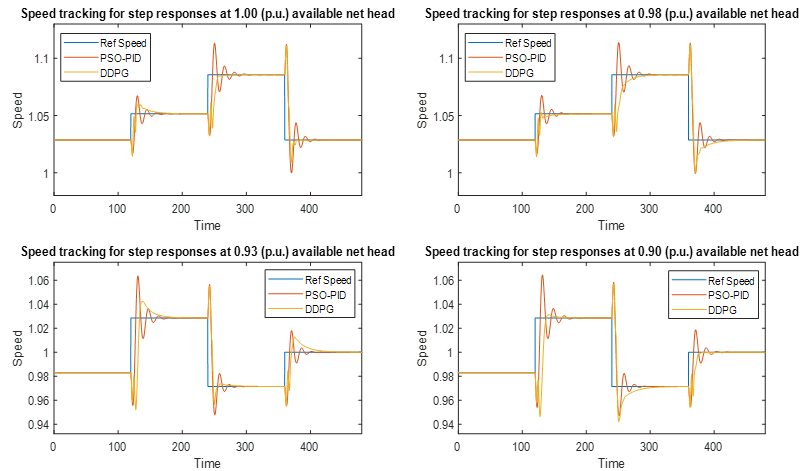
The primary frequency control (PFC) capability of the designed DDPG governor was tested and compared with the PID governor on the IEEE 9-bus system. To simulate a disturbance in the system, a 5% and 10% load change was implemented at bus 5 at t = 10s as shown in Figure 7. For the 5% increase in the load at bus 5, the frequency response of both governors was identical, but as the load at bus 5 was increased by 10%, the DDPG governor exhibited a faster response at the inertia response region compared to the PID governor. Also, a fixed-frequency droop control approach was employed to react to the disturbance.

5. Conclusion

This paper demonstrated a step-by-step approach to using reinforcement learning techniques to design a DDPG-based governor for the turbine of an ASPSH. The FFNN employed by the actor was able to achieve an optimal policy capable of controlling the gate of the turbine while accounting for the changing system dynamics. The DDPG agent demonstrated an excellent tracking capability like the PSO-PID, but in some cases, it was able to reach a steady state faster than the PSO-PID with lesser overshoot. This slight improvement in the settling time contributed to a slightly faster response in the primary frequency control with the DDPG agent as the magnitude of the grid disturbance increased.

The primary advantage of the proposed DDPG-based governor is that, unlike the conventional PID controller, it eliminates the need for tuning and retuning the controller parameters as system dynamics change. Since the DDPG agent is trained with measured data from the system, it can be updated over time to account for the decrease in the system efficiency that is related to aging.

The DDPG-based governor in this research was done with a single penstock PSH plant, future work could be to consider a PSH unit with multiple penstocks as well as accounting for the water level in the surge tanks as it is another component that contributes to the complexity of the turbine regulation.

References

[1] J. Culberg, M. Negnevitsky, and K. M. Muttaqi, "Hydro-turbine governor control: theory, techniques and limitations," presented at the Australasian Universities Power Engineering Conference (AUPEC 2006), 2006.

[2] J. Godjevac, "Comparison between PID and fuzzy control," 1993.

[3] "The Negative Consequences of Poor PID Controller Tuning," Control Automation. https://bit.ly/3GyVMLe.

4] R. Lowe, Y. Wu, A. Tamar, J. Harb, P. Abbeel, and I. Mordatch, "Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments," 2017, doi: 10.48550/ARXIV.1706.02275.

[5] T. P. Lillicrap, J. J. Hunt, A. Pritzel, N. Heess, T. Erez, Y. Tassa, D. Silver, and D. Wierstra, "Continuous control with deep reinforcement learning." arXiv, Jul. 05, 2019. Accessed: Jan. 01, 2023. [Online]. Available: View Article

[6] Q. Huang, W. Hu, G. Zhang, D. Cao, Z. Liu, Q. Huang, and Z. Chen, "A novel deep reinforcement learning enabled agent for pumped storage hydro‐wind‐solar systems voltage control," IET Renew. Power Gener., vol. 15, no. 16, pp. 3941-3956, Dec. 2021, doi: 10.1049/rpg2.12311. View Article

[7] G. Zhang, W. Hu, D. Cao, J. Yi, Q. Huang, Z. Liu, Z. Chen, and F. Blaabjerg, "A data-driven approach for designing STATCOM additional damping controller for wind farms," Int. J. Electr. Power Energy Syst., vol. 117, p. 105620, May 2020, doi: 10.1016/j.ijepes.2019.105620. View Article

[8] G. Zhang, W. Hu, D. Cao, S. Jing, Q. Huang, and Z. Chen, "Deep Reinforcement Learning Based Optimization Strategy for Hydro-Governor PID Parameters to Suppress ULFO," in 2020 5th International Conference on Power and Renewable Energy (ICPRE), Shanghai, China, Sep. 2020, pp. 446-450. doi: 10.1109/ICPRE51194.2020.9233119. View Article

[9] S. Nag and K. Y. Lee, "DFIM-Based Variable Speed Operation of Pump-Turbines for Efficiency Improvement," IFAC-Pap., vol. 51, no. 28, Art. no. 28, 2018, doi: 10.1016/j.ifacol.2018.11.788. View Article

[10] G. Abad, Ed., Doubly fed induction machine: modeling and control for wind energy generation. Hoboken, NJ: IEEE Press, 2011. View Article

[11] D. Silver, G. Lever, N. Heess, T. Degris, D. Wierstra, and M. Riedmiller. "Deterministic policy gradient algorithms". In Proceedings of the 31st International Conference on International Conference on Machine Learning, vol 32 (ICML'14). JMLR.org, I-387-I-395.

[12] "Markov decision process," Wikipedia, 22-Dec-2022. [Online]. Available: https://en.wikipedia.org/wiki/Markov_decision_process. [Accessed: 04-Jan-2023].

[13] D. Cao, W. Hu, J. Zhao, G. Zhang, Z. Liu, Z. Chen, and F. Blaabjerg, Reinforcement learning and its applications in modern power and energy systems: a review, Journal of Modern Power Systems and Clean Energy 8 (6) (2020) 1029e1042. View Article

[14] G. Zhang, W. Hu, D. Cao, Q. Huang, Z. Chen, and F. Blaabjerg, "A novel deep reinforcement learning enabled sparsity promoting adaptive control method to improve the stability of power systems with wind energy penetration," Renewable Energy, vol. 178, pp. 363-376, 2021. View Article

[15] "Deep deterministic policy gradient," Deep Deterministic Policy Gradient - Spinning Up documentation. [Accessed: 04-Jan-2023]. [Online]. Available: View Article