Volume 1 - Year 2020 - Pages 1-10
DOI: 10.11159/jmids.2020.001
Robust Adaptive Control for Uncertain Wearable Exoskeleton Robot Using Time Delay Estimation
Brahim brahmi1, Maarouf Saad1, Youcef Saidi2, Cristobal Ochoa-Luna3, Mohammad H. Rahman4
1École de technologie Supérieure Montréal, Canada
brahim.brahmi.1@ens.etsmtl.ca; Maarouf.Saad@etsmtl.ca
4Department of Electrical Engineering, Faculty of Technology
University of Moulay Tahar, Algeria
saidi_youcef_20@yahoo.com
3School of Engineering and Science
Instituto Tecnológico y de Estudios Superiores de Monterrey Aguascalientes, Mexico
cristobal.ochoa.luna@itesm.mx
4Mechanical/Biomedical Engineering Department
University of Wisconsin-Milwaukee Milwaukee, WI, USA
rahmanmh@uwm.edu
Abstract - This paper presents a new Integral Second-Order Terminal Sliding Mode Control incorporating Time Delay Estimation applied to passive rehabilitation protocols of an exoskeleton robot with dynamics uncertainties and unknown bounded disturbances. The use of second-order sliding mode is due to its attractive characteristics of accuracy, attenuation of chattering and fast convergence. However, its problem is that the unknown dynamics of the exoskeleton robot and external disturbances caused by its different wearers can be amplified by the second derivative of the sliding surface, which leads to instability of the exoskeleton system. Using Time Delay Estimation will estimate the uncertain dynamics while overcoming the main limitation of second-order sliding mode. The stability analysis is formulated and proved based on Lyapunov function. Experimental results with a healthy subject confirm the effectiveness of the proposed control.
Keywords: Rehabilitation robots, Second Order Sliding Mode; Time Delay Estimation, Passive assistive motion.
© Copyright 2020 Authors - This is an Open Access article published under the Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received: 2018-10-24
Date Accepted: 2020-01-17
Date Published: 2020-03-04
NOMENCLATURE
![]() Joints position
Joints position
![]() Joints velocity
Joints velocity
![]() Joints acceleration
Joints acceleration
![]() Inertia matrix,
Inertia matrix,
![]() Coriolis and centrifugal matrix
Coriolis and centrifugal matrix
![]() Gravitational vector
Gravitational vector
![]() Control input
Control input
![]() External disturbances
External disturbances
![]() Known inertia matrix,
Known inertia matrix,
![]() Known Coriolis/centrifugal matrix
Known Coriolis/centrifugal matrix
![]() Known gravity vector
Known gravity vector
![]() Known dynamic model
Known dynamic model
![]() Unknown dynamic model
Unknown dynamic model
![]() ̂Estimated of dynamic model
̂Estimated of dynamic model
![]() Time delay error
Time delay error
![]() Sliding surface
Sliding surface
![]() Position error
Position error
![]() Lyapunov function
Lyapunov function
1. Introduction
Recently, the use of physiotherapy rehabilitation robots has shown great potential for improving the patient's disability and independence of function [1]. Control of these kind of robots presents additional complexity over the control of conventional robotic manipulators due to their complex mechanical structure designed for human use, the types of desired tasks, and the sensibility of the interaction with a large diversity of human wearers [1]. As a result, these conditions, make the robot system vulnerable to dynamics uncertainties and external disturbances.
Sliding mode control (SMC) is one of the most popular control strategies that is widely applied on robotics systems thanks to its attractive characteristics of robustness to the dynamics nonlinear-uncertainties and external disturbances [2]. However, conventional SMC suffers from two major shortcomings. The first one is that SMC ensures an asymptotic convergence to the equilibrium without finite-time convergence. Many control techniques have been developed to overcome this problem such terminal sliding mode control (TSMC) [3]. This later utilizes a nonlinear switching surface to guarantee the finite time convergence by including a fractional order, which allows to the states trajectories to converge to equilibrium faster. In literature, the accuracy performance of TSMC is improved by proposing a new approach for instance, fast TSMC [4] and non-singular TSMC [5]. A second major problem is that SMC is fundamentally based on a larger high-gain switching controller which pushes the system state to converge to the equilibrium. Nevertheless, the high-activity switching gain causes an undesirable “chattering” dilemma which can damage the actuators of the robot system [6].
Recently, many conventional approaches were developed to avoid the undesirable chattering problem; e.g. by exchanging the discontinuous function by a continuous function (as a saturation function). Second Order Sliding Mode Controller (SOSMC) [7] is considered as one of the efficient approaches dedicated to eliminate chattering problem and provide a high performance’s precision. Additionally, various approaches have been developed to improve the performance of SOSMC such Twisting control and Super-Twisting control [8]. The main idea of SOSMC is to allow a sliding surface and its consecutive derivative to go to zero and to maintain the discontinuous control under an integral function, which can eliminate the undesirable chattering. Nevertheless, the second-time derivative of the sliding surface might produce instability of the system, a risk that the nonlinear uncertainties and external disturbances amplify. Recently, Second Order Terminal Sliding mode Control (SOTSMC) was introduced to provide a great control performance to deal with a chattering phenomenon and provide a finite time convergence [9, 10]. So, to the best of our knowledge, no SOTSMC with integral action has been proposed before to solve the mentioned problems.
Motivated to deal with the mentioned problem, and based on our previous work [11, 12], we proposed a new integral Second Order Terminal Sliding mode controller (ISOTSMC) combined with Time Delay Estimation (TDE) [12] to provide a good approximation of the uncertainties and the bounded external disturbances of an exoskeleton robot. TDE uses time-delayed knowledge about the previous system state and its control input to provide an accurate estimation of unknown dynamics. The incorporation of integral control relies on its attractive characteristics, where it has delivered good performance with conventional SMC [13]. The control scheme aims to keep the high precision of the SOSMC, eliminate the chattering problem, and provide a finite-time convergence to equilibrium.
The remainder of the paper is organized as follows. The dynamics of the robot is presented in the next section. The control scheme is described in section 3. Experimental results and some comparisons are given in section 4. Finally, the conclusion is presented in section 5.
2. Characterization of system rehabilitation
2. 1. Exoskeleton Robot Development
The developed exoskeleton robot ETS-MARSE (École de technologie supérieure - Motion Assistive Robotic-exoskeleton for Superior Extremity) is a redundant robot consisted of 7-degrees of freedom (DOFs), as shown in Fig. 1. It was created to provide assistive physiotherapy motion to the injured upper limb. The idea of the designed exoskeleton is basically extracted from the anatomy of the upper limb of the human, to be ergonomic for their wearer along the physiotherapy session. The shoulder part consists of three joints, the elbow part comprises by one joint and the wrist part consists of three joints. Each part responsible for performing a variety of upper limb motions. All special characteristics of the ETS-MARSE, the modified Denavit-Hartenberg (DH) parameters (Table 1), and comparison with similar existing exoskeleton robots are summarized in [14].
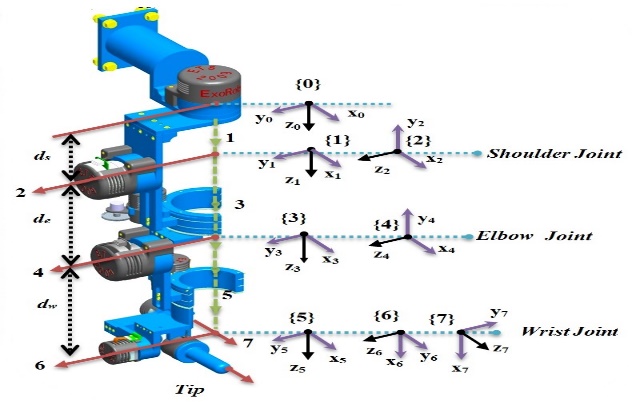
Table 1. Modified Denavit-Hartenberg Parameters
| Joint (i) | αi-1 | ai-1 | di | θi |
| 1 | 0 | 0 | ds | θ1 |
| 2 | -p/2 | 0 | 0 | θ2 |
| 3 | p/2 | 0 | de | θ3 |
| 4 | -p/2 | 0 | 0 | θ4 |
| 5 | p/2 | 0 | dw | θ5 |
| 6 | -p/2 | 0 | 0 | θ5-p/2 |
| 7 | -p/2 | 0 | 0 | θ7 |
The workspace of the designed robot is given in Table 2.
Table 2. Workspace ETS-MARSE.
| Joints | Motion | Workspace |
| 1 | Shoulder joint horizontal flexion/extension |
0°/140° |
| 2 | Shoulder joint vertical flexion/extension | 140°/0°3 |
| 3 | Shoulder joint internal/external rotation | -85°/75° |
| 4 | Elbow joint flexion/extension | 120°/0° |
| 5 | Forearm joint pronation/supination | -85°/85° |
| 6 | Wrist joint Ulnar/radial deviation |
-30°/20° |
| 7 | Wrist joint flexion/extension | -50°/60° |
2. 2. Dynamics of ETS-MARSE Robot
The dynamics of ETS-MARSE is expressed as follows:
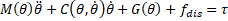
where ![]() ,
, ![]() , and
, and ![]() are respectively the joints position, velocity,
and acceleration vectors,
are respectively the joints position, velocity,
and acceleration vectors,![]() ,
, ![]() , and
, and ![]() are respectively the symmetric
positive-definite inertia matrix, the Coriolis and centrifugal vector, and the
gravitational vector including the user’s arm and the exoskeleton arm.
are respectively the symmetric
positive-definite inertia matrix, the Coriolis and centrifugal vector, and the
gravitational vector including the user’s arm and the exoskeleton arm. ![]() is the torque vector,
is the torque vector, ![]() is the external disturbances vector. Without
loss of generality, the dynamic model (1) can be rewritten as follows:
is the external disturbances vector. Without
loss of generality, the dynamic model (1) can be rewritten as follows:
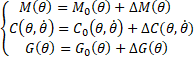
where ![]()
![]() , and
, and ![]() are respectively the known inertia matrix, the
Coriolis/centrifugal matrix, and the gravity vector.
are respectively the known inertia matrix, the
Coriolis/centrifugal matrix, and the gravity vector. ![]() ,
,![]() , and
, and ![]() are the uncertain parts. Let us introduce a new
variable such that:
are the uncertain parts. Let us introduce a new
variable such that: ![]() and
and![]() ; hence, the dynamic model expressed in Eq. 1
can be rewritten as follows:
; hence, the dynamic model expressed in Eq. 1
can be rewritten as follows:
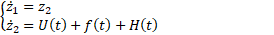
where, ![]()
![]() and
and ![]() This notation is used to facilitate the handling
of the control methodology with:
This notation is used to facilitate the handling
of the control methodology with: ![]() ;
; ![]() , and
, and ![]() .
.
2.3. Problem Statement
The developed approach aims to set up a new integral Second-Order Terminal Sliding mode control (ISOTSMC) to improve the performance of conventional second-order SMC and to ensure the finite-time convergence of the sliding surface. Since the dynamic parameters of the robot are unknown, the integration of TDE to estimate them ensures a desirable performance. The control strategy is developed to be able to complete the passive rehabilitation movement by obtaining a control input that forces the measured trajectory to track the desired trajectory even if the robot operates with uncertain dynamics and unforeseen external disturbances.
Property 1: The known
part of inertia matrix ![]() is symmetric and positive definite for all
is symmetric and positive definite for all![]() [2].
[2].
Assumption 1: The function
![]() is globally Lipschitz function.
is globally Lipschitz function.
Assumption 2: The desired trajectory is bounded.
Assumption 3: The external
disturbance ![]() is supposed to be continuous, has finite
energy, and satisfies
is supposed to be continuous, has finite
energy, and satisfies![]() , with an unknown positive disturbance boundary
, with an unknown positive disturbance boundary![]() .
.
3. Control Design
The first step in the control development is to define the surface S in terms of position error. Then, select the integral terminal type of the sliding surface, where this later must be stable and guarantee the finite-time convergence. Let us chose the integral terminal surface as follows:
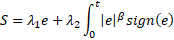
where ![]() is the position error and
is the position error and ![]() is the measured and desired trajectory respectively, where
is the measured and desired trajectory respectively, where ![]() ,
, ![]() where
where ![]() ; and
; and ![]() . Taking the first-time derivative of
. Taking the first-time derivative of![]() , we find:
, we find:
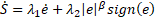
Theorem 1: Considering the exoskeleton robot system (Eq. 3) that satisfies the mentioned properties and assumptions, the selected surface (Eq. 4) is stable and finite-time independently of the initial state.
Proof: Let us consider the following Lyapunov function:
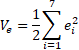
where ![]() is the initial value of the selected Lyapunov function. The
time derivative of Eq. 6 can be obtained by:
is the initial value of the selected Lyapunov function. The
time derivative of Eq. 6 can be obtained by:
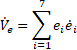
Let us assume that ![]() is provided, from Eq. 5 we can obtain the
following expression using scalar form as follows:
is provided, from Eq. 5 we can obtain the
following expression using scalar form as follows:
Substituting Eq. 8 into Eq.7 we have:
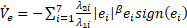
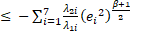
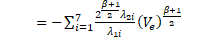
where ![]() . Therefore,
. Therefore, ![]() is verified. We can rewrite Eq. 9 as follows:
is verified. We can rewrite Eq. 9 as follows:
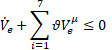
where ![]() and
and ![]() , taking into consideration that
, taking into consideration that ![]() and
and ![]() . So, according to [15], the convergence of the finite time
. So, according to [15], the convergence of the finite time ![]() can be given by:
can be given by:
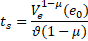
where ![]() is the Lyapunov function’s initial value. The proof is
complete.
is the Lyapunov function’s initial value. The proof is
complete.
Remark 1: It is obvious from Eq.
11 that the initial value of the Lyapunov function ![]() and the ratio
and the ratio ![]() manage the finite time convergence
manage the finite time convergence ![]() of the selected sliding surface. A large value of
of the selected sliding surface. A large value of ![]() can ensure a short convergence time. Likewise, too large
gain ratio may produce an overshoot influence. Therefore, the trade-off between
fast convergence and control performance is required to choose
can ensure a short convergence time. Likewise, too large
gain ratio may produce an overshoot influence. Therefore, the trade-off between
fast convergence and control performance is required to choose ![]() and
and ![]() .
.
While the selected surface is chosen, the combination of ISOTSMC with TDE can be easily making up now. Let us take the second-time derivative of Eq. 5 as:
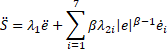
Substituting Eq. 8 into Eq. 12, we obtain:

To solve Eq. 13, the integral terminal super-twisting controller is given as follows:
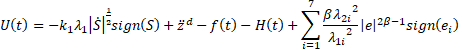
With ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() .
.
Practically, as established, all dynamic parameters of the
exoskeleton robot are not easily obtained due to the uncertainties and their
variation during the robot’s tasks. Since ![]() is uncertain it might influence the control
proposition. From now on, we will consider
is uncertain it might influence the control
proposition. From now on, we will consider ![]() uncertain. If Assumption 1 is verified, we can
used TDE [11] to estimate
uncertain. If Assumption 1 is verified, we can
used TDE [11] to estimate ![]() as follows:
as follows:
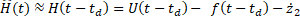
where, ![]() is a very-small time delay constant.
Practically, the smallest constant that can be achieved in real time is the
sampling period. According to the Lipschitz condition (Assumption 1), the time
delay error can be calculated as follows:
is a very-small time delay constant.
Practically, the smallest constant that can be achieved in real time is the
sampling period. According to the Lipschitz condition (Assumption 1), the time
delay error can be calculated as follows:
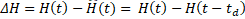
where ![]() is the Lipschitz constant.
is the Lipschitz constant.
Remark 2: It can be seen from Eq.16 that if Assumption 2 is verified, the estimation error of the uncertainties and disturbances is always bounded by the Lipschitz constant.
Theorem 2: Considering the exoskeleton robot system (Eq. 3) which satisfies the mentioned properties and assumptions, the control law of Integral Second-Order Terminal Sliding Mode Control incorporating TDE ensures the convergence of the sliding surface and its first and second derivative to zero in finite-time given by:

where ![]() and
and ![]() , where
, where ![]() . Whenever the following conditions are verified:
. Whenever the following conditions are verified:
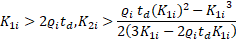
Proof: Before selecting the Lyapunov function candidate, let us substitute the control law (Eq. 17) into Eq.13, we find:
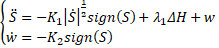
It can be seen that Eq. 19 has the same
structure as the Super-Twisting control [8]. Let us now introduce new variables such that: ![]() and
and![]() . The system (Eq. 19) becomes as follows:
. The system (Eq. 19) becomes as follows:
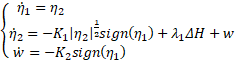
To ensure the convergence of the robot system (Eq. 3), we will assume the following Lyapunov function candidate:
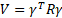
where ![]() ,
, ![]() . The Lyapunov function (Eq. 21) is chosen to be
continuous and non-differentiable at
. The Lyapunov function (Eq. 21) is chosen to be
continuous and non-differentiable at ![]() [16]. It is
positive-definite and radially-bounded by choosing an appropriate matrix
[16]. It is
positive-definite and radially-bounded by choosing an appropriate matrix ![]() such that,
such that,
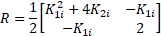
with,
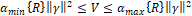
where ![]() are the minimum and maximum eigenvalues of
are the minimum and maximum eigenvalues of ![]() and
and ![]() is the Euclidian norm of
is the Euclidian norm of ![]() . Taking the
derivative of Lyapunov function (Eq. 21):
. Taking the
derivative of Lyapunov function (Eq. 21):
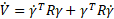
The time derivative of ![]() can be
defined as follows:
can be
defined as follows:
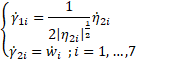
Using Eq.20 and Eq. 24,
we can rewrite ![]() in matrix form, where
in matrix form, where![]() :
:
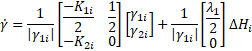
The above equation can be written in the form:
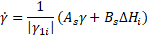
where, ![]() . Substituting Eq. 26 into Eq. 23, we find:
. Substituting Eq. 26 into Eq. 23, we find:
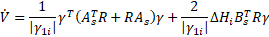
Since ![]() is positive from Eq. 16. The following
inequality can be established:
is positive from Eq. 16. The following
inequality can be established: ![]() , where:
, where:
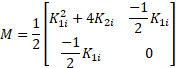
Therefore Eq.27 becomes as:
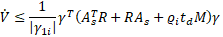
The above Eq. 28 can be rewrite as follows:
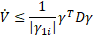
where ![]() is written such that
is written such that ![]() , and
, and ![]() is calculated such that:
is calculated such that:
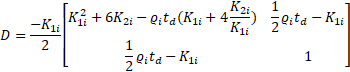
The function ![]() is negative definite if
is negative definite if ![]() . This selection will ensure that the
. This selection will ensure that the ![]() . While
. While ![]() is positive and symmetric. In such case, we can
rewrite Eq. 29 as:
is positive and symmetric. In such case, we can
rewrite Eq. 29 as:
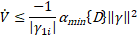
where ![]() is the minimum eigenvalue of
is the minimum eigenvalue of ![]() . Eq. 30 proves that Lyapunov function is
semi-negative definite. Now, let us prove the finite time convergence of the
system. From Eq. 22, we have:
. Eq. 30 proves that Lyapunov function is
semi-negative definite. Now, let us prove the finite time convergence of the
system. From Eq. 22, we have:
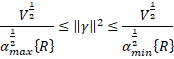
It is clear that: ![]() and from Eq. 30 and Eq. 31, we have:
and from Eq. 30 and Eq. 31, we have:
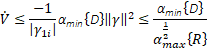
According to this equation, the finite time convergence of the sliding surface can be obtained such that:
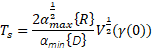
The diagram block of the proposed controller is given in Fig.2.
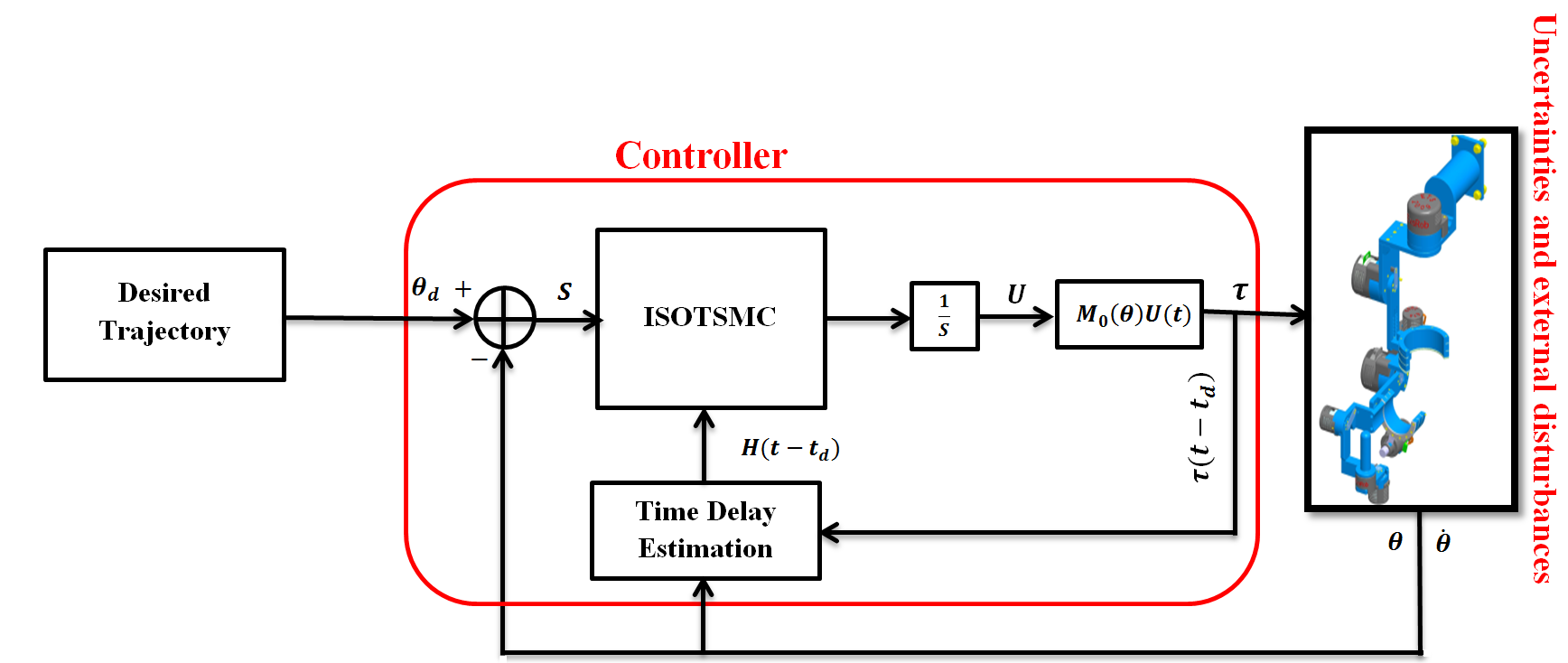
4. Experiment and Comparative Study
The robot system consists of three processing units, the first is a PC where the top-level commands are sent to the robot using a LabVIEW interface, i.e. the control scheme selection. This PC also receives the data after the robot task is executed to analyze its performance. The other two processing units are part of a National Instruments PXI platform. Firstly, a NI-PXI 8081 controller card with an Intel Core Duo processor; in this card, the main operating system of the robot and the top-level control scheme are executed. In our case, the ISOTSMC based controller as well as the estimation based on time delay approach, at a sampling time of 500µs. Finally, at input/output level, a NI PXI-7813R remote input/output card with a FPGA (field programmable gate array) executes the low-level control; i.e. a PI current control loop (sampling time of 50 µs) to maintain the current of the motors required by the main controller. Also, in this FPGA, the position feedback via Hall-sensors (joint position) and basic input/output tasks are executed. Each joint of the ETS-MARSE is powered by a brushless DC motor (Maxon EC-45, EC-90 ) combined with harmonic drives (gear ratio 120:1 for motor-1, motor-2, and motor-4 and gear ratio 100:1 for motor-3 and motors 5–7). The General schematic of the experimental architecture is depicted in Fig. 3.
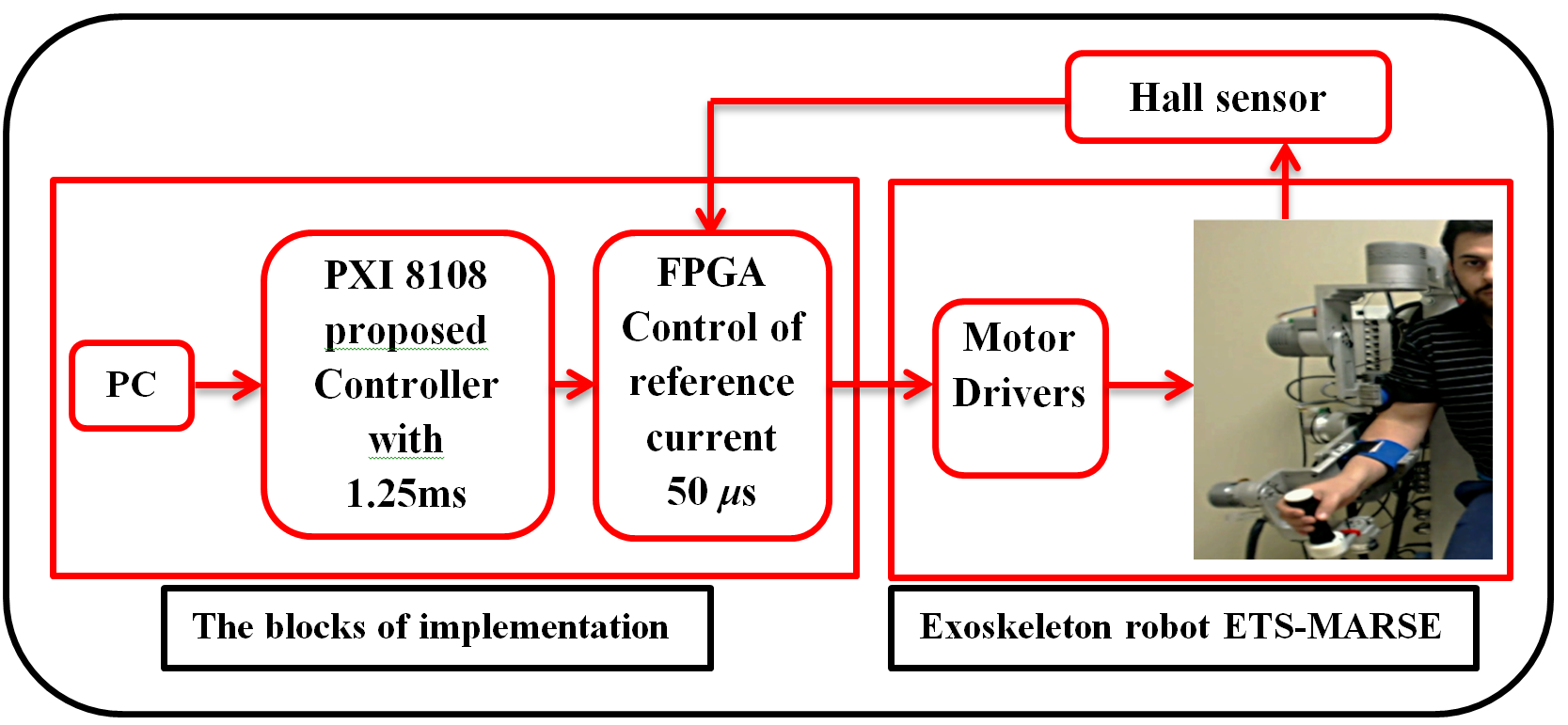
An experiment session was created to validate
the proposed control approach. It consists on an exercise performed with a
healthy subject with an age of 30 years, height of 177 cm, and weight of 75 Kg.
In this case, the trajectory is repeated three times for each movement with the
speed varying between (28 deg/sec for joint-3 and 48 deg/sec for the remaining
joints). The results of the task are illustrated in Fig. 4. A Second exercise
is given in cartesian space as rectangular form(Initial position to Target-A forward to
Target-B Target-C then return to Initial position). The initial position of
the robot is given with the elbow joint position at 90 degrees. The control
gains are chosen manually as follows: ![]() ,
, ![]() ;
; ![]() ,
, ![]() ,
, ![]() .
.
4. 1. Joint space results
We can appreciate in Fig. 4 that for the movement of all joints, the desired trajectory (represented by the red line), practically overlaps the measured trajectory (represented by the solid blue line). It is clear from the plots in this figure that the proposed controller provides an excellent performance. Where, the controller has the potential to maintain stability of the system along the designed therapeutic movement with a position error (second column of Fig. 2) less than three degrees for all joints. The last column of Fig. 2 shows the control input which is clearly smooth and without the chattering effect. We can conclude that the controller is robust; it offers a very good performance despite the high speed and unknown parameters of the robot.
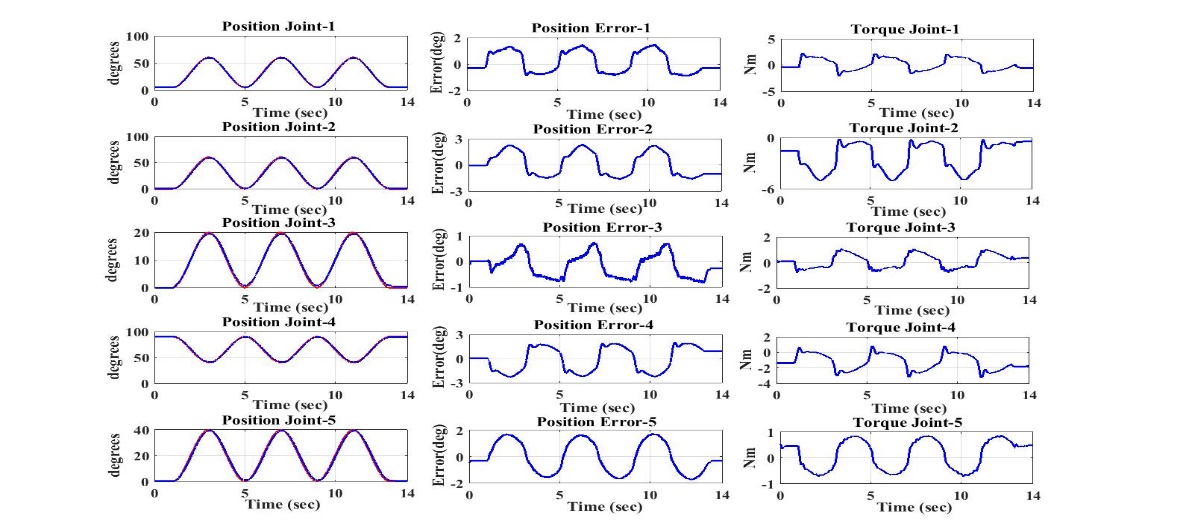
4. 1. Cartesian space results
In order to maneuver the exoskeleton in Cartesian space, we used the inverse Jacobian matrix method, since the proposed control is executed in the joint space. Due to the redundant nature of the ETS-MARSE robot where its Jacobian matrix is not quadratic, the inverse kinematics can be solved using the pseudo-inverse of the Jacobian, which can be expressed as follows:
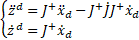
where ![]() is the desired Cartesian position and
orientation vector of the end-effector, and
is the desired Cartesian position and
orientation vector of the end-effector, and ![]() are the Cartesian desired acceleration and
velocity vectors, respectively.
are the Cartesian desired acceleration and
velocity vectors, respectively. ![]() are the calculated joint acceleration and velocity
respectively, and
are the calculated joint acceleration and velocity
respectively, and ![]() is pseudo-inverse generalized. The proposed joint-space
based control in this paper does not need a Jacobian matrix or inversion of a
Jacobian matrix, as for a Cartesian space-based controller. The role of the
Jacobian matrix and its inverse here is the generation of the desired
rehabilitation trajectory. Hence, the singularity is not an issue in this case.
Moreover, the singularities of the exoskeleton robot are known to us; they will
appear when the ETS-MARSE is straight down (θ2 = 0°, and/or θ4 = 0°,
and/or θ6 = −90°). As well, a singularity will happen when the axes
of rotation of joint-1 (Z1), and joint-3 (Z3), and/or joint-5 (Z5), and/or
joint-7 (Z7) are aligned with each other. By knowing these cases, we can easily
define the trajectory by avoiding all kinematics singularities.
is pseudo-inverse generalized. The proposed joint-space
based control in this paper does not need a Jacobian matrix or inversion of a
Jacobian matrix, as for a Cartesian space-based controller. The role of the
Jacobian matrix and its inverse here is the generation of the desired
rehabilitation trajectory. Hence, the singularity is not an issue in this case.
Moreover, the singularities of the exoskeleton robot are known to us; they will
appear when the ETS-MARSE is straight down (θ2 = 0°, and/or θ4 = 0°,
and/or θ6 = −90°). As well, a singularity will happen when the axes
of rotation of joint-1 (Z1), and joint-3 (Z3), and/or joint-5 (Z5), and/or
joint-7 (Z7) are aligned with each other. By knowing these cases, we can easily
define the trajectory by avoiding all kinematics singularities.
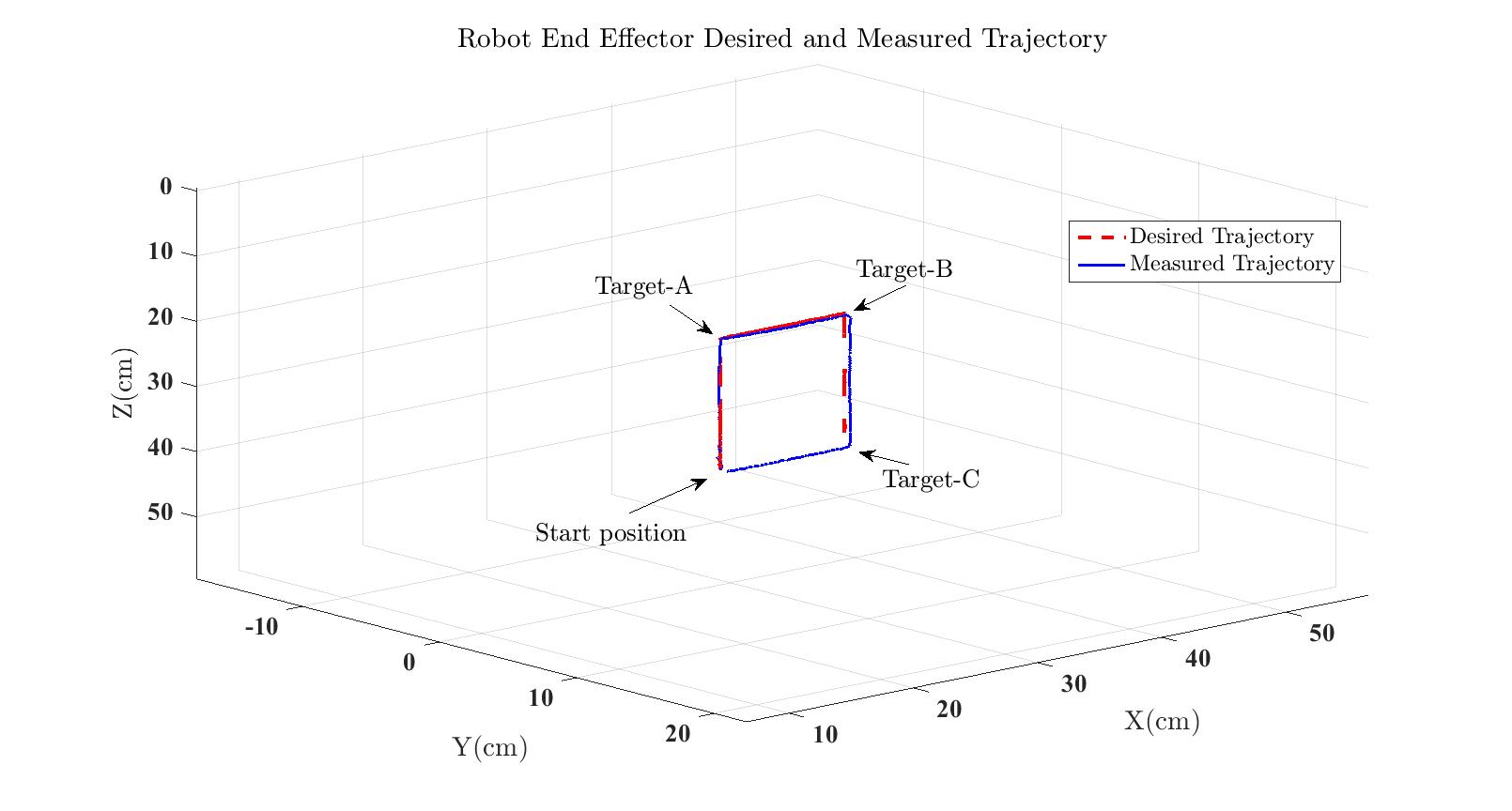
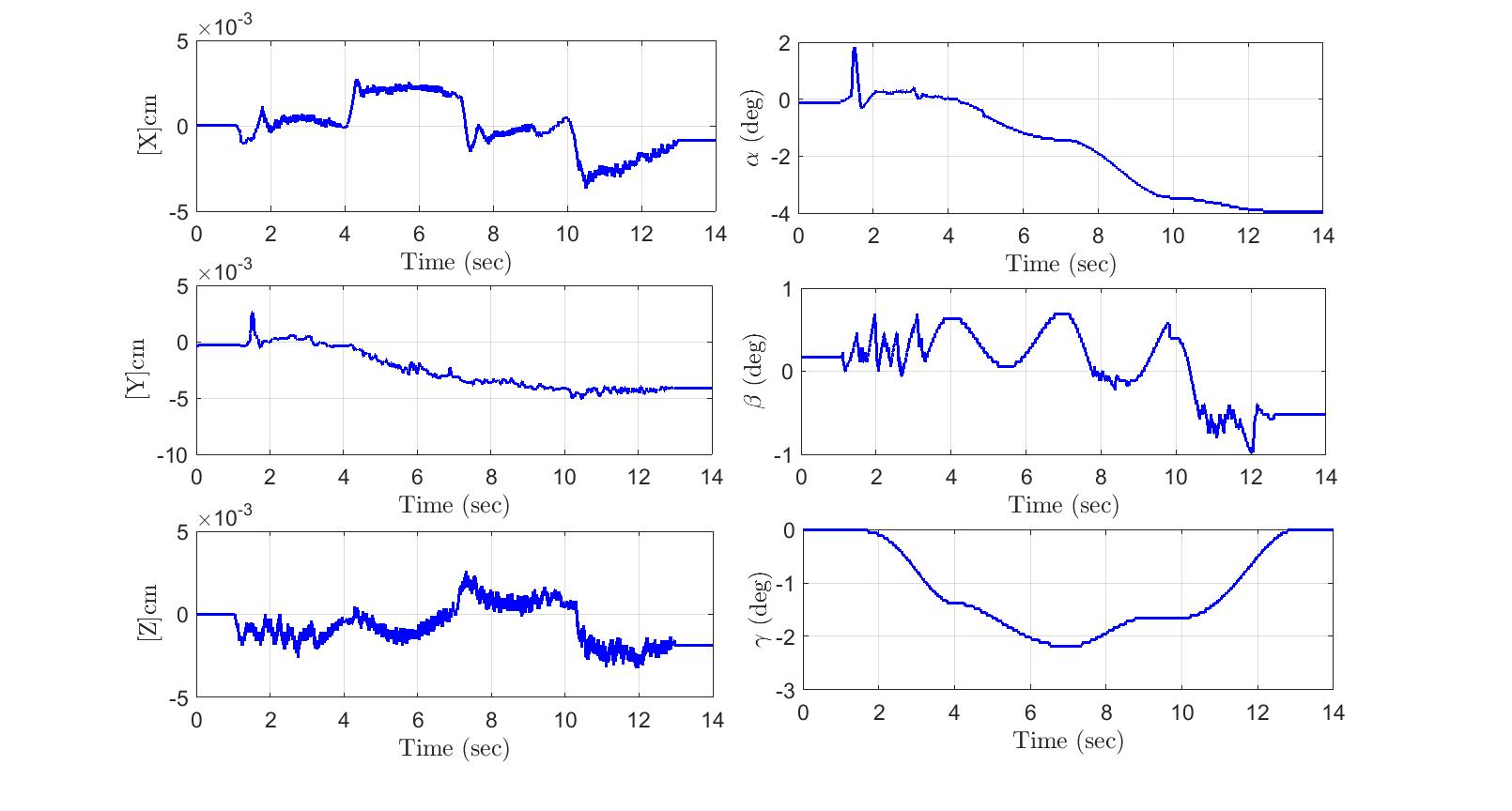
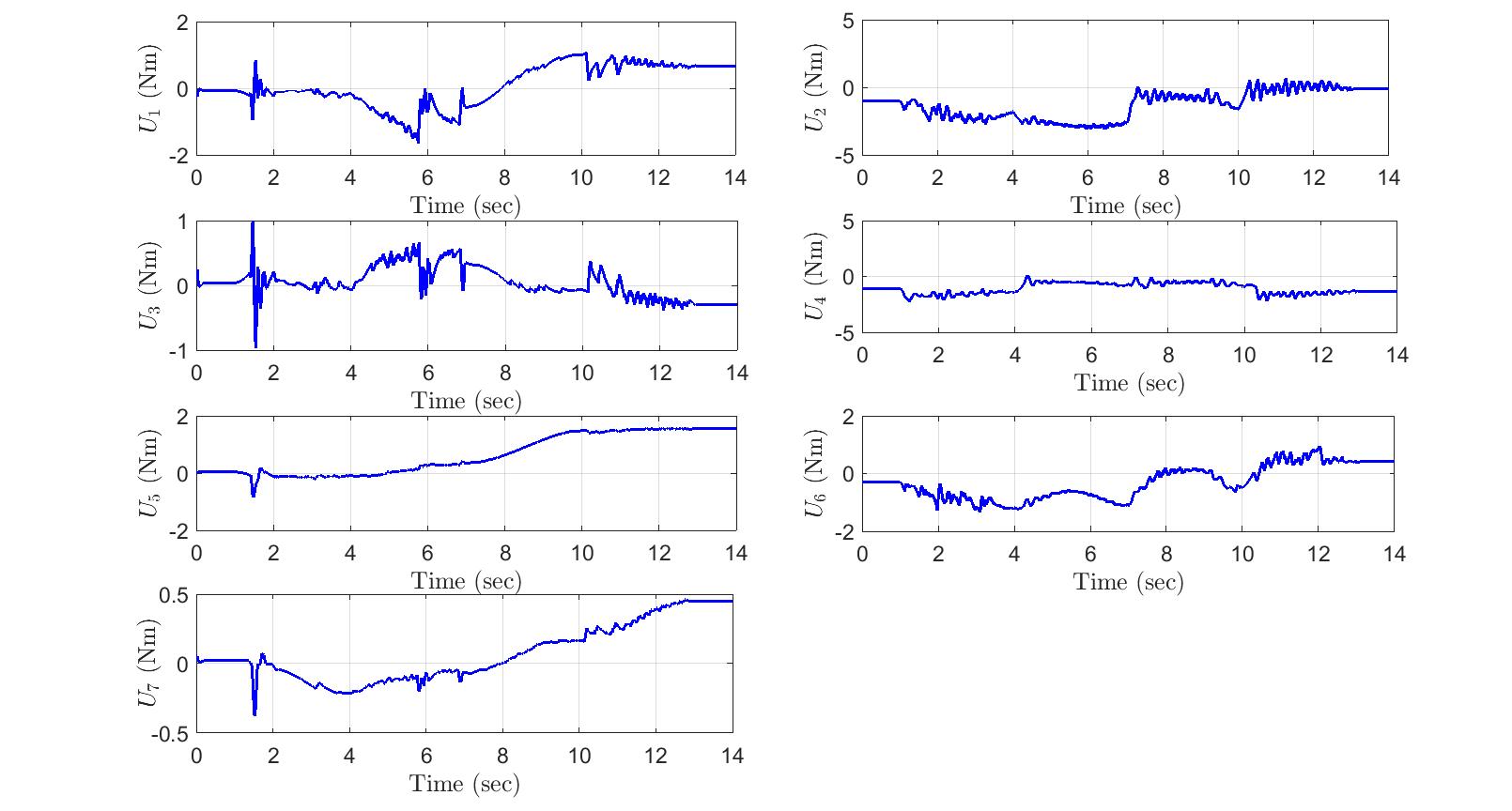
It is obvious from (Figs.5-7) performed by subject-A, the controller provides satisfactory results with small errors (Fig.6) of position and acceptable control input (Fig.7). Where, the controller forces the performed trajectory to converge to the desired trajectory. These results reflect the robustness of the proposed control with unknown dynamics model of the robot and in presence of variable or unexpected external disturbances (physiological condition of the subject-A).
To
show more of the feasibility of the designed strategy, we propose a numerical
comparison between the above controllers (conventional controller and proposed
controller) by calculating the root mean square (RMS) of the error and the
control input of each controller as follows: ![]() and
and ![]() , where N is the number of samples of the signals,
corresponding with the time steps of the trial. The evaluation of the
controller is given in Table 3.
, where N is the number of samples of the signals,
corresponding with the time steps of the trial. The evaluation of the
controller is given in Table 3.
Table 3. Controllers evolution.
| Controller | RMS (error) | RMS (Torque) |
| ISOTSMC | 0.0150 | 2.0728 |
| SOSMC | 0.0988 | 3.2147 |
It is clear from Table 3 that the proposed controller achieves an excellent performance with small value of overall RMS error, compared with the conventional SOSMC, even the dynamic model of the exoskeleton is not completely known, and in presence of external forces.
5. Conclusion
In this paper, we investigated the control applied to passive rehabilitation protocol of an exoskeleton robot by presenting a new integral second-order terminal sliding mode incorporating time delay estimation. Using second-order sliding mode is due to its attractive characteristics of fast convergence, accuracy, and attenuation of chattering. However, its problem is that the unknown dynamic of the exoskeleton robot and external disturbances can be amplified by the second derivative of the sliding surface, which leads to instability of the robot system. Applying TDE to estimate the unknown dynamics and external disturbances permits chattering reduction.
The proposed controller presents an excellent performance both joint and Cartesian spaces. These results are confirmed by the small tracking errors as shown in Table 3.
The controller is dedicated to improve the robustness of the second-order sliding mode control while overcoming its main limitation. Where, the proposed control deals very well with the unknown dynamic and external payload presented by the subject’s arm. The stability analysis is formulated and demonstrated based on Lyapunov function. An experimental physiotherapy session with a healthy subject was created to test the effectiveness and feasibility of the proposed control, which are proved.
References
[1] S. Xie, "Advanced Robotics for Medical Rehabilitation," Springer Tracts in Advanced Robotics, vol. 108, pp. 1-357, 2016.
[2] J.-J. E. Slotine and W. Li, Applied nonlinear control vol. 199: Prentice hall Englewood Cliffs, NJ, 1991.
[3] Y. Wu, X. Yu, and Z. Man, "Terminal sliding mode control design for uncertain dynamic systems," Systems & Control Letters, vol. 34, pp. 281-287, 1998.
[4] X. Yu and M. Zhihong, "Fast terminal sliding-mode control design for nonlinear dynamical systems," IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, vol. 49, pp. 261-264, 2002.
[5] Y. Feng, X. Yu, and Z. Man, "Non-singular terminal sliding mode control of rigid manipulators," Automatica, vol. 38, pp. 2159-2167, 2002.View Article
[6] L. M. Fridman, "An averaging approach to chattering," IEEE Transactions on Automatic Control, vol. 46, pp. 1260-1265, 2001.View Article
[7] A. Levant, "Principles of 2-sliding mode design," automatica, vol. 43, pp. 576-586, 2007.View Article
[8] T. Gonzalez, J. A. Moreno, and L. Fridman, "Variable gain super-twisting sliding mode control," IEEE Transactions on Automatic Control, vol. 57, pp. 2100-2105, 2012.
[9] S. Ding, J. Wang, and W. X. Zheng, "Second-order sliding mode control for nonlinear uncertain systems bounded by positive functions," IEEE Transactions on Industrial Electronics, vol. 62, pp. 5899-5909, 2015.
[10] L. Zhao, J. Huang, H. Liu, B. Li, and W. Kong, "Second-order sliding-mode observer with online parameter identification for sensorless induction motor drives," IEEE Transactions on Industrial Electronics, vol. 61, pp. 5280-5289, 2014.View Article
11] B. Brahmi, M. Saad, C. Ochoa-Luna, and M. H. Rahman, "Adaptive control of an exoskeleton robot with uncertainties on kinematics and dynamics," in Rehabilitation Robotics (ICORR), 2017 International Conference on, 2017, pp. 1369-1374.
[12] B. Brahmi, M. Saad, C. O. Luna, P. Archambault, and M. Rahman, "Sliding mode control of an exoskeleton robot based on time delay estimation," in Virtual Rehabilitation (ICVR), 2017 International Conference on, 2017, pp. 1-2.
[13] A. M. Shotorbani, A. Ajami, S. G. Zadeh, M. P. Aghababa, and B. Mahboubi, "Robust terminal sliding mode power flow controller using unified power flow controller with adaptive observer and local measurement," IET Generation, Transmission & Distribution, vol. 8, pp. 1712-1723, 2014.
[14] M. H. Rahman, M. J. Rahman, O. Cristobal, M. Saad, J.-P. Kenné, and P. S. Archambault, "Development of a whole arm wearable robotic exoskeleton for rehabilitation and to assist upper limb movements," Robotica, vol. 33, pp. 19-39, 2015.
[15] H. Wang, Z.-z. Han, Q.-y. Xie, and W. Zhang, "Finite-time chaos synchronization of unified chaotic system with uncertain parameters," Communications in Nonlinear Science and Numerical Simulation, vol. 14, pp. 2239-2247, 2009.
[16] J. A. Moreno and M. Osorio, "A Lyapunov approach to second-order sliding mode controllers and observers," in Decision and Control, 2008. CDC 2008. 47th IEEE Conference on, 2008, pp. 2856-2861.

