Volume 5 - Year 2024 - Pages 65-73
DOI: 10.11159/jmids.2024.008
A Stackelberg Differential Game Framework for Enhancing Energy Efficiency in Satellite Communication Systems
Wei Wan1, Yuanyuan Peng2, John M Cioffi3, Kalia T. Glover4
1,2,4Claflin University, Department of Mathematics and Computer Science
400 Magnolia Street, Orangeburg, SC, USA, 29115
wwan@claflin.edu; ypeng@claflin.edu; kalglover@claflin.edu
3Stanford University, Department of Electrical Engineering
350 Jane Stanford Way, Stanford, CA, USA, 94305
cioffi@stanford.edu
Abstract - The multiple-user terminals in a satellite transponder’s communication channel compete for limited radio resources to meet their own data rate needs. Because inter-user interference limits on the satellite transponder’s performance, the transponder’s power-control system needs to coordinate all its users to reduce interference and maximizes overall performance of this channel. This paper studies Stackelberg competition among the asymmetrical users in a transponder’s channel, where some users called leader have priority to choose their power control strategy, but other users called followers have to optimize their power control strategy with given leader’s controls. A Stackelberg Differential Game (SDG) is set up to model the Stackelberg competition in a transponder’s communication channel. Each user’s utility function is a trade-off between transmission data rate and power consumption. The dynamics of the system is the changing of channel gain. The optimality condition of Stackelberg equilibrium of leaders and followers is a set of Differential Algebraic Equations (DAE) with an imbedded control strategies from its counterpart. In order to solve for Stackelberg equilibrium, an algorithm based on optimizing leaders’ and followers’ Hamiltonians iteratively is developed. The numerical solution of the SDG model provides the transponder’s power control system with each user’s power-control strategy at the Stackelberg equilibrium.
Keywords: Stackelberg Differential Game, Spectrum and Power Allocation, Energy-Efficiency, Satellite Communication.
© Copyright 2024 Authors - This is an Open Access article published under the Creative Commons Attribution License terms. Unrestricted use, distribution, and reproduction in any medium are permitted, provided the original work is properly cited.
Date Received:2024-02-01
Date Revised: 2023-07-15
Date Accepted: 2024-08-03
Date Published: 2024-09-30
Nomenclature

1. Introduction
This paper studies satellite communication channels. The first important feature of satellite communication channel is interference. Each satellite transponder represents an individual communication channel. Within a 36-MHz bandwidth channel, each transponder can handle an enormous amount of information by using different multiple-access schemes, so each channel contains many pairs of senders and receivers [1], [2]. This study assumes each pair is selfish to maximize its own performance by a specific power-allocation scheme. The interference from other pairs affects the channel performance [3]. Satellites most commonly use the C band (6/4 GHz), and the C band’s heavier use leads to more interference. Shifting satellite communication to higher frequencies is one effective way to minimize interference, but crowding and interference problems will still exist, which motivates this study to develop a technique that increases bandwidth efficiency and signal-caring capacity, and decreases interference of satellite communication subsystems. The second important feature of satellite communication is long distance, which implies the dynamic and controllable feature of channel gain has to be considered when modelling the transponder’s communication channel. The third important feature of a satellite transponder, which is interesting and studied in this paper is the existence of Stackelberg competition in this channel. The status of users in a channel are not always same. Some users called leader have priority to select their power control strategy, which implies other users called followers have to optimize with the given leader’s control strategy. Thus, it is interesting to study how the leaders take advantage of this opportunity to improve their utility, and how the followers survive better.
This paper models a transponder’s communication channel as an interference channel with aim to optimize the trade-off between transmission data rate and power consumption. Section II reviews a transponder’s communication channel and existing energy-efficient power control game models. Section III models the power-allocation optimization problem for all users in a transponder as a Stackelberg Differential Gaussian Interference Channel Game (SDGICG) based on the special properties of satellite wireless communications. Section IV and Section V derive and analyse the SDGICG model’s optimality condition, and develop numerical methods to solve for Stackelberg equilibrium and then solve the model. The numerical solution from the model provides all users in a transponder’s channel with the optimal power-allocation scheme at the Stackelberg equilibrium.
2. Preliminaries
2. 1. Satellite Wireless Communications Subsystem
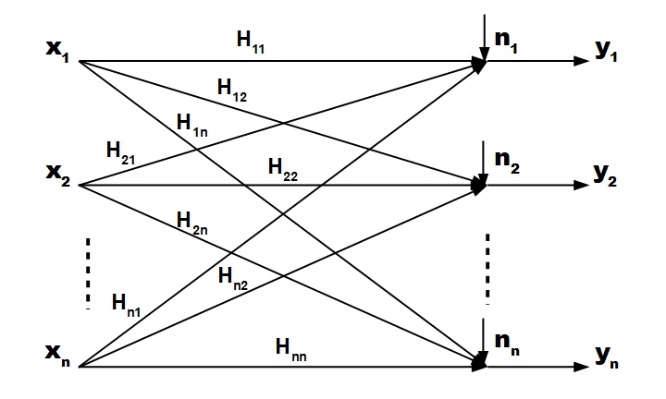
A transponder is a repeater that implements a wideband communication channel that can carry many simultaneous one-to-one communication transmissions [1], so it can be modelled as a multiuser interference channel as Fig. 1 [4], [5]. This interference channel is an M-to-M network where a one-to-one correspondence exists between senders and receivers such that each sender communicates information only to its corresponding receiver [4]. This study models each pair of sender-receiver in a transponder channel as a user (a player). The interference limits the system’s performance. Interference cancellation is an option when the interference signal is sufficiently strong, but its implementation is complex, requiring prior knowledge of users’ transmission schemes is accessible by other users [5], [6]. This study assumes that each user applies power to affect the cross-coupling gain and then reduce interference without any interference cancellations.
2. 2. Static Power Control Game
Goodman and Mandayam [7] study a static energy-efficient power control game on a distributed multiple-access channel with a finite number of users, denoted by K. Each user chooses its own power control policy pi to maximize its energy-efficiency ui=(Ri f(SINRi))/pi , where Ri is the information transmission rate in bit/s for user i, and f is an efficiency function representing the block success rate, which is assumed to be sigmoidal and identical for all the users [7], [8].
It is called a static game because (a) it assumes that the users transmit data over quasi-static or block-fading channels at the same time and in the same frequency band, assuming each channel gain Hi (n) to be constant over each block. (b) Each user in the game applies a fixed power policy, once per block, to maximize its utility. However, for long-distance wireless communication such as satellite communication, channel gain varies with time, so its modulus is usually assumed to be in a compact set |Hi|2∈[ηimin,ηimax]. A variable power policy is expected to be designed to control channel gain. Furthermore, with assumption of complete information and rationality, the existence of Nash Equilibrium is guaranteed by Debreu-Fan-Glicksberg existence theorem [9]. The Nash Equilibria are found by solving equations ![]() . And the static power game has unique pure Nash Equilibrium, which is discussed by Yates [10], and Saraydar [11].
. And the static power game has unique pure Nash Equilibrium, which is discussed by Yates [10], and Saraydar [11].
Besides the energy-efficient game for communication channel, there are other types of noncooperative games constructed for different utility, which are generally called Gaussian Interference Games (GIGs) [12], [13]. The water-filling algorithm also solves for Nash Equilibrium of GIG without the need for centralized control [13]. Amir Leshem applied cooperative game theory for analysing interference channels [14]. Wei Wan created a cooperative static game for a transponder’s centralized power control to maximize overall channel data transmission rate [15].
2. 3. Non-cooperative vs Stackelberg Differential Game (DG)
In non-cooperative DG models, all the competitors make decision at the same time, and their controls are combined in the same dynamics. No competitor has knowledge of the strategies of others as he decides on his own. The player i’s objective function is
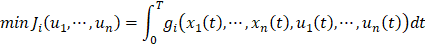
, and all competitors’ controls are combined in the same dynamics:
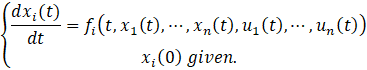
The most interesting solution of non-cooperative DG model is Nash Equilibrium. Optimality condition for Nash Equilibrium of non-cooperative DG is a set of Differential-Algebraic Equations (DAE). Wei Wan and John Cioffi [16] set up a non-cooperative Differential Game (DG) to model the users’ competition in a transponder’s communication channel. In this game model, each user’s energy efficiency is redefined, and logistic growth is adopted to approximate the changing of channel gain under specific energy consumption. The objective function of each user is a weighted sum of energy efficiency and targeted channel gain. Then, the optimality condition for Nash Equilibrium of the model is derived. At last, an algorithm is developed to solve for Nash Equilibrium. The design of algorithm is based on a steep-descent method and optimizes all players’ objective functions simultaneously.
Stackelberg game provides a model for a system where the status of competitors is not same. Stackelberg game is played as follows in Fig. 2.

The users who select control first are leader. The leader first announces his control policy u. Then, the other users who are able to observe leader’s control u and then select their controls are followers. The followers select their control v* by solving ![]() . In the end, the leaders select their optimal control
. In the end, the leaders select their optimal control ![]() by solve
by solve ![]() .
.
Furthermore, when controls are combined in a dynamic system, above game is played as Stackelberg Differential Game (SDG). The leader announces at time t=0 that he will use the control u(x(t),t) for t∈[0,T]. Then, the follower has to take the leader’s control path as given and selects his own control v(x(t),t) to minimize his objective functional
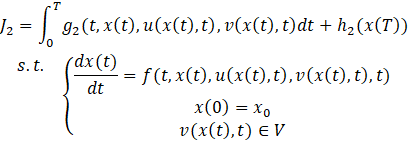
Thus, there exists a set-valued mapping:
F:U→V
by Fu={v∈V│v=argmin[J2 (u,v)] }. From Pontryagin minimum principle, if an optimal v exists, with v∈Fu, we must have a function λ:[0,T]→Rn such that
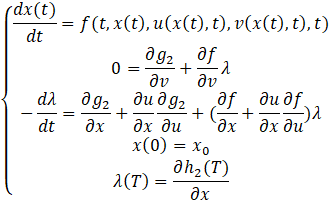
For v∈Fu, the leader’s problem is to select his control u(x,t) to minimize his objective function
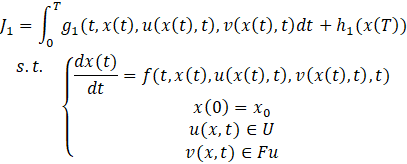
, which can be written explicitly as follows:
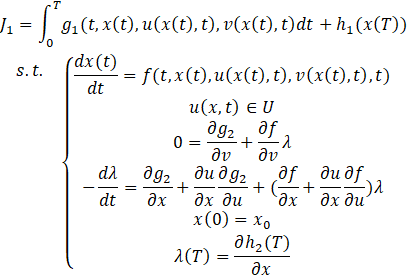
By solving above problem, the optimal control u(x,t) for the leader could be obtained, and then solving the follower’s optimal control problem to get his optimal control v(x,t).
3. Stackelberg Differential Game for a Transponder
In the process of designing power-control policy, it is assumed that some users in one satellite transponder’s channel have priority over others in terms of the order of making decision. That is there exists Stackelberg competition when allocating power among the users in this channel.
Each pair of (xi,yi),i∈κ represents a user in a transponder’s channel. All users choose their power-control policy before establishing communication. Each user’s communication is through N sub-frequency channels simultaneously, and each user applies independent power control policy in each sub-frequency channel. Furthermore, each user has two types of power consumption policy: the first improves its own channel gain, and the second decreases interference. Stackelberg differential game is modelled as follows.
Construction of objective function: Since the first and most interesting objective for each user in this transponder is to optimize the trade-off between the achievable data rate and energy consumption. With an assumption of no channel interference cancellation, the interference from other users is consequently noise. Then, the achievable rate for player i at time t over frequency (f1,f2) is as follows [5], [3]:
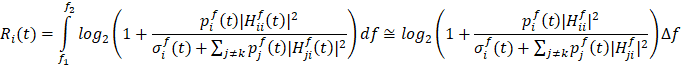
, where approximation assumes the variables to be constant over small bands. The energy efficiency for user i,i∈κ over time [0,T] is
,which is the log transformation of ratio of information bits that are transmitted without error per unit time to the transmit power. It is to be maximized. The second goal of transponder power control is for the direct channel gain to reach a certain channel-capacity level and also to reduce the cross-coupling gain to certain level. This second objective is to minimize the following expression:
, where ![]() are weights between different
objectives;
are weights between different
objectives; ![]() are constants, and upper bounds of
are constants, and upper bounds of ![]() ; and
; and ![]() are targeted channel-gain levels.
are targeted channel-gain levels.
Construction of dynamics: Generally, ![]() belong to a compact set
belong to a compact set ![]() , and can be approximated by
Kronecker’s delta function [17]. In satellite wireless communication, satellite
transponders can apply energy
, and can be approximated by
Kronecker’s delta function [17]. In satellite wireless communication, satellite
transponders can apply energy ![]() to impact and control channel gain.
The analysis in this paper assumes that the growth rate is proportional to
power consumption. Thus, logistic growth with carrying capacity is adopted to
approximate the dynamics of
to impact and control channel gain.
The analysis in this paper assumes that the growth rate is proportional to
power consumption. Thus, logistic growth with carrying capacity is adopted to
approximate the dynamics of ![]() :
:
, where ![]() is a constant, and presents the
growth rate.
is a constant, and presents the
growth rate. ![]() is the fixed constant over frequency
is the fixed constant over frequency ![]() for
user
for
user ![]() ,
which stands for the proportion of
,
which stands for the proportion of ![]() , used by user
, used by user ![]() to
increase channel gain. Furthermore, when user
to
increase channel gain. Furthermore, when user ![]() applies
applies
![]() to improve the channel gain
to improve the channel gain ![]() , it also increases the cross-coupling
gain
, it also increases the cross-coupling
gain ![]() . Furthermore, user
. Furthermore, user ![]() is
able to cost power
is
able to cost power ![]() to decrease interference brought by
to decrease interference brought by ![]() . At last, because of threshold
effects existing in channel gain, cross-coupling gain has a lower bound. Thus,
the dynamics of
. At last, because of threshold
effects existing in channel gain, cross-coupling gain has a lower bound. Thus,
the dynamics of ![]() is approximated by:
is approximated by:
where i ≠ j, and βif represents the growth rate, ξif is the lower bound of cross-coupling gain. In order to save space, xii(t), xij(t) stand for |Hiif(t)|2, |Hijf(t)|2, respectively. After the objective function, control, and dynamics of the system are defined, the SDGICG model (κ, {pif}i ∈ κ, {Ji}i ∈ κ) is played according to (3)-(6).
4. Solution of SDGICG Model
There are two methods to solve SDGICG
models. The first one is based on solving (6). If the control ![]() could
be solved from
could
be solved from ![]() , the following nonclassical optimal
control problem is obtained:
, the following nonclassical optimal
control problem is obtained:
By solving the above optimal control problem, the optimal control u(x,t) for the leader is obtained, and then the follower’s optimal control problem is solved to get his optimal control v(x,t). The obvious disadvantage of this method is: (1) the solvability of control v. (2) Deriving optimality condition for (12) is challenging, which is usually Differential Algebraic Equations and is difficult to solve [18].
The second method is iterative method.
The design of this method is based on the procedure of how Stackelberg game is
played in Fig. 2. In the beginning, leader and follower initiate a control ![]() over
over ![]() for themselves, respectively. With
their controls, the dynamics of the system is solved and then their objective
functions
for themselves, respectively. With
their controls, the dynamics of the system is solved and then their objective
functions ![]() are evaluated. Next, with this
leader’s control being unchanged and embedded in the follower’s dynamics, the
follower searches for an optimal control
are evaluated. Next, with this
leader’s control being unchanged and embedded in the follower’s dynamics, the
follower searches for an optimal control ![]() to optimize its objective function.
Next, with this follower’s optimal control being embedded in the leader’s
dynamics, the leader searches for its optimal control
to optimize its objective function.
Next, with this follower’s optimal control being embedded in the leader’s
dynamics, the leader searches for its optimal control ![]() to optimize its objective function
to optimize its objective function ![]() . Then, we calculate the improvement
of leader’s objective function values between this step and the first step:
. Then, we calculate the improvement
of leader’s objective function values between this step and the first step: ![]() . If the difference is small enough (
. If the difference is small enough (![]() ), then the searching procedure stops.
Otherwise, the leader’s updated optimal control
), then the searching procedure stops.
Otherwise, the leader’s updated optimal control ![]() is embedded in the follower’s dynamics,
and follower begins to another search for its optimal control
is embedded in the follower’s dynamics,
and follower begins to another search for its optimal control ![]() . The procedure continue until
leader’s objective function values has no/little improvement. Above iterative
procedure is exhibited in Fig. 3.
. The procedure continue until
leader’s objective function values has no/little improvement. Above iterative
procedure is exhibited in Fig. 3.
Based on above iterative procedure, an iterative algorithm is developed to solve the SDGICG model (Algorithm 1). In Step 2 of Algorithm 1, after follower embeds leaders’ discretized control to solve its own game model, the iterative algorithm in [16] is used and embedded. In Step 3, the iterative algorithm in [16] is also used to solve for leader’s optimal control.
Algorithm 1:
Step 1: Leader and follower initiate a random discrete control
{uL(f,j)(k)} and {uF(f,j)(k)} over t ∈ [0, T].
uL(f,j)(k) = uL(f,j)(t), t ∈ [tk, t(k+1)), k = 1, ⋅⋅⋅, M
uF(f,j)(k) = uF(f,j)(t), t ∈ [tk, t(k+1)), k = 1, ⋅⋅⋅, M
where f = 1, …, N. j stands for the jth iteration, and set j = 0.
Then, solve the dynamics and calculate both the leader's and follower’s objective function values: JLj and JFj.
Step 2: The follower embeds the leader’s discretized control {uL(f,j)(k)} to solve his own game model for an optimal control {uF(f,j+1)(k)}, and calculates the follower’s objective function values: JF(j+1).
Step 3: The leader embeds the follower’s optimal control {uF(f,j+1)(k)} to solve his own game model for {uL(f,j+1)(k)} and calculates his state variable values and his objective function value JL(j+1).
Step 4: Check if |JLj - JL(j+1)| < ε, then stop, and output {uL(f,j+1)(k)} and {uF(f,j+1)(k)}; otherwise, set j = j + 1 and go back to Step 2.
5. Numerical Experiments
A two-player SDGICG over one sub-frequency channel is solved by Algorithm 1. The numerical experiment aims to study the effects of the cost of power on Stackelberg Equilibrium. The values of parameters are in Table 1 and Table 2.
Comparing the values of parameters in Table 1, these two players are symmetric/same except for the cost of power ci and the order of selecting their power control policies. The relation c1 > c2 implies player 1’s cost of power is more expensive than player 2. And in this game, player 1 is the leader, and player 2 is the follower. Other parameters have the same values for both players. The relation of weights w1(i) > w2(i) implies both players prefer the direct channel gain to reach a certain channel-capacity level rather than reducing the cross-coupling gain to a certain level. The value of riif = 0.9 implies both players aim to reach 90% of channel-gain capacity at the end of the game, and rjif = 0.3 implies they aim to reduce cross-coupling gain to 30% of channel-gain capacity at the end of the game.
TABLE 1. PARAMETERS OF OBJECTIVE FUNCTIONS
| Player 1 - Leader | Player 2 - Follower | ||
|---|---|---|---|
| c1 | 6 | c2 | 4 |
| σ1 | 0.2 | σ2 | 0.2 |
| w1(1) | 2 | w1(2) | 2 |
| w2(1) | 1 | w2(2) | 1 |
| r11(1) | 0.9 | r22(2) | 0.9 |
| r21(1) | 0.3 | r12(2) | 0.3 |
The parameters in Table 2 are constants. αi, βij are growth rates of channel gain. These values are chosen for the numerical experiment, and αi > βij shows that the growth rate of direct channel gain is larger than the cross-coupling gain. The value of τi shows that user i uses half of its control to increase channel gain and the other half to reduce cross-coupling gain. The ηii, ηij are upper bounds of direct channel gain and cross-coupling gain, respectively. The numerical relation ηii > ηij exhibits the property of a standard communication channel. The value of ξij is the lower bound of cross-coupling gain and is close to zero. The initial values of state variables are given by xii(0), xij(0), and the relation xii(0) ≫ xij(0) reflects the relation between direct channel and cross-coupling gain in real communication channels.
TABLE 2. PARAMETERS OF DYNAMICS
| Player 1 - Leader | Player 2 - Follower | ||
|---|---|---|---|
| α1 | 6 | α2 | 6 |
| β12 | 3 | β21 | 3 |
| τ1 | 0.5 | τ2 | 0.5 |
| η11 | 1 | η22 | 1 |
| η12 | 0.5 | η21 | 0.5 |
| ξ12 | 0.001 | ξ21 | 0.001 |
| x11(0) | 0.1 | x22(0) | 0.1 |
| x12(0) | 0.02 | x21(0) | 0.02 |
Convergence of the algorithm is shown by the convergence of the leader’s objective functions in Fig. 4, where |JL(n+1) - JL(n)| ≈ 1 × 10-7. In each iteration, the vanishing of dHi/dpif is observed: ‘‖dHL/dpL1‖ ≈ 3.5 × 10-7, ‖dHF/dpF1‖ ≈ 1 × 10-5. The total number of iterations for the leader is 8 (Fig. 4).
Two players’ optimal controls at Stackelberg Equilibrium are given in Fig. 5. The most important feature of optimal controls is that both players compete intensely at the beginning of the game, and reduce competition level gradually over time. Furthermore, Leader’s competition level is always lower than follower’s. This is explained by first-mover advantage of leader, and the cost of player 1’s control is higher than follower.
Two players’ direct channel gain at Stackelberg Equilibrium behave similar and approach to the channel carrying capacity (Fig. 6). The follower’s direct channel gain level is slightly higher than leader’s. It is expected that the cost of follower’s control is cheaper with other parameters of these two players being at the same level.
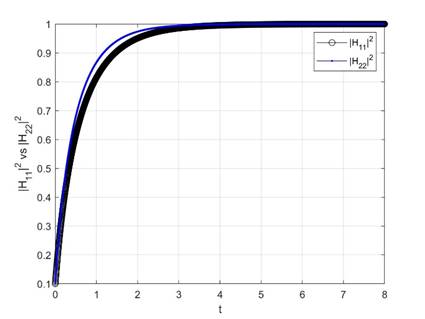
Figure 6. Trajectories of Direct Channel Gain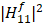 and
and 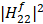
In the end, it is interesting to observe that the cross-coupling gain of these two players behaves differently (Fig. 7). The leader’s interference to the follower (|H12f|2) increases slightly, but |H21f|2 increases sharply over time. This can be understood since the cost for the follower is cheaper, allowing the follower to apply more power to reduce the leader’s interference with the follower.
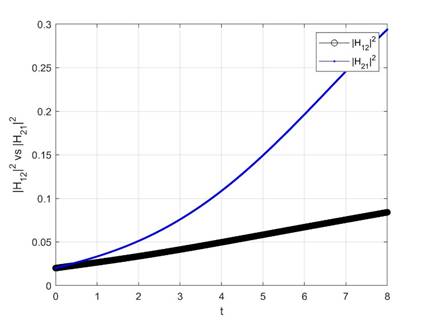
Figure 7. Comparison of 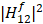 and
and 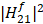
6. Summary and Conclusion
This paper is a continuing study of a satellite transponder’s communication channel following [16], [19]. It aims to improve energy efficiency by studying the power allocation of satellite transponder’s channel. In satellite communication subsystems, the performance of each pair of transmitters and receivers depends not only on its own power allocation, but also on the other pairs’. Each user in the transponder’s channel would be competing for limited radio resources to meet their selfish data rates with less energy consumption. Another feature of satellite communication is its long-distance, so the channel gain is not constant. Thus, each user is able to apply energy to improve its own channel gain and reduce interference. This paper introduced a SDGICG model for all users in one transponder’s communication channel. It is assumed that the status of these users are not same: some users have priority to select their power control policy. In the setup of the game model, energy efficiency, dynamics of channel gain, and the objective function of each user follows [16]. The optimality condition for follower’s decision problem is an optimal control problem with imbedded leader’s controls, and leaders’ problem is to search for their optimal control with imbedded followers’ optimal controls. An iterative algorithm is developed to solve the SDGICG model. In each iteration, the algorithm from [19] which is based on steep-descent method to search for optimal control is imbedded. Numerical experiment shows this algorithm is effective and efficient to solve the SDGICG model. The numerical solution of the game model can be used to support designing power allocation scheme of transponders with Stackelberg competition. In the end, one limitation of research work in this paper is proof of existence and uniqueness of Stackelberg equilibrium. Continuing research is necessary and expected since we need to guarantee the convergency of the iterative algorithm: the existence of followers’ optimal control with the imbedded leader’s control; the existence of leaders’ optimal control with the embedded followers’ optimal control.
Acknowledgements
This research is supported by NSF Award No. 1900984 and No. 2346698. We thank NSF’s support. We thank our colleagues from Stanford University and Claflin University who provided insight and expertise that greatly assisted the research。
References
[1] L. Frenzel, "Satellite Communication," in Principles of Electronic Communication Systems, McGraw-Hill Education, 2007, pp. 670-708.
[2] I. T. Union, Handbook on Satellite Communications, 3rd Edition, Wiley, April 2002.
[3] M. L. T. S. L. M. D. Mehdi Bennis, "Spectrum Sharing Games on the Interference Channel," in IEEE International Conference on Game Theory for Networks, Turkey. 8 p. hal-00447056, May 2009.
[4] C. AYDANO, "Interference channels," IEEE Transactions on Information Theory, Vols. IT-24, no. 1, pp. 60-70, 1978. View Article
[5] P. G. J. Zhao Yue, "Optimal Spectrum Management in Multiuser Interference Channels," University of California, Los Angeles, 2008-11-21.
[6] A. L. Ilai Bistritz, "Game Theoretic Dynamic Channel Allocation for Frequency-Selective Interference Channels," in The 42nd IEEE International Conference on Acoustics, Speech and Signal Processing, 2017.
[7] M. N. Goodman D.J., "Power control for wireless data," in IEEE Pers. Commun., 2000. View Article
[8] M. N. G. D. Shah V., "Power control for wireless data based on utility and pricing," in IEEE Proceedings of the 9th International Symposium on Indoor and Mobile Radio Commun. (PIMRC), 1998.
[9] H. T. Samson Lasaulce, Game Theory and Learning for Wireless Networks: Fundamentals and Applications, Academic Press, October 3, 2011. View Article
[10] Y. R.D., "A framework for uplink power control in cellular radio systems," IEEE J. Sel. Areas Commun., vol. 13, no. 7, p. 1341-1347, 1995. View Article
[11] M. N. G. D. Saraydar C.U., " Efficient power control via pricing in wireless data networks," IEEE Trans. Commun., vol. 50, no. 2, p. 291-303, 2002. View Article
[12] A. L. Amir Laufer, "Distributed coordination of spectrum and the prisoner's dilemma," Proc. of the First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks - DySPAN, 2005.
[13] G. G. a. J. M. C. Wei Yu, "Distributed Multiuser Power Control for Digital Subscriber Lines," IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, vol. 20, no. 5, pp. 1105-111, JUNE 2002. View Article
[14] E. Z. Amir Leshem, "Cooperative Game Theory and the Gaussian Interference Channel," IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, vol. 26, no. 7, pp. 1078-1087, SEPTEMBER 2008. View Article
[15] Y. P. N. M. Wei Wan, "Study of Optimal Power Control by Cooperative Game for Satellite Communication Subsystems," in Proceedings of the 6th International Conference on Communication and Electronics Systems, 2011.
[16] J. M. C. Y. P. S. H. Wei Wan, "Differential Game Analysis of Energy Efficiency for Satellite Communication Subsystems," in 2023 Fifth International Conference on Advances in Computational Tools for Engineering Applications, Lebanon, 2023.
[17] U. E. A. Leshem, "The Interference Channel Revisited: Aligning Interference by Adjusting Antenna Separation," IEEE Transactions on Signal Processing, vol. 69, pp. 1874-1884, 2021. View Article
[18] W. W. Negash Medhin, "Leader-Follower Games in Marketing: A Differential Game Approach," International Journal of Mathematics in Operational Research, vol. 2, no. 2, pp. 151-177, 2010. View Article
[19] J. M. C. Y. B. H. Wei Wan, "Study of Energy Efficiency for Satellite Communication Subsystems by Differential Game," in PROCEEDINGS OF THE 10thINTERNATIONAL CONFERENCE ON CONTROL, DYNAMIC SYSTEMS, AND ROBOTICS (CDSR 2023), Ottawa,Canada, June 01, 2023 -June 03, 2023.

