Journal of Machine Intelligence and Data Science (JMIDS)

1. Introduction

Imprecise and dependent information can be found in various real case studies, with one of the most common applications being related to expenditures. In this paper, we will present a case study on tourism expenditure, providing a real data example. Dealing with dependent and imprecise information raises several issues that must be considered in both prediction and clustering frameworks. One of the main issues raising while analysing these kinds of data is the possibility that many individuals may spend nothing or very little during certain parts of their journey, leading to a high incidence of zeros in the data.

This paper presents an overview of the issues and solutions found in the existing literature and it is structured as follows. In Section 2 will be discussed and presented the kind of imprecise and dependent information with a focus of the tourism field given a real example data in sub-section 2.1. In Section 3 will be presented the economic theories at the basis of dependent expenditure, the main supervised and unsupervised machine learning algorithms used so far to analyse imprecise and dependent information. Conclusions and future directions are presented in the final section.

2. Imprecise and dependent information: the case of the tourism sector

The economic impact of tourism flows is often essential for those regions/local communities in which tourism is considered the major source of income [1]. To improve the economic effects of tourism visits, appropriate data and tools are needed to study the determinants of tourism expenditure and to analyse the tourists’ spending behaviour in depth.

Studies on tourism demand have generally focused on the macroeconomic dynamics. Nevertheless, as stated for instance by Alegre and Pou [2], even though the micro-level perspective has been seldom analysed (e.g., see [3]–[5]), it provides several advantages over the macro-level studies. Among others, the micro-level approach makes it possible to observe individual choices regarding the consumption of a tourism commodity or service, and to analyse the heterogeneity and diversity that characterize individual tourism consumption behaviour. See [6] for an extensive review of the most common microeconomic models adopted in recent microdata studies.

The main advantage in adopting a micro-level approach is the possibility to simultaneously consider both the consumer behaviour theory on the decision-making process to purchase, and the neoclassical economic theory of budget constraint.

Specifically, the consumer behaviour theory assumes that the individual purchase process for a tourism good or service is a two-decision process [7], i.e. the decision to purchase something followed by the decision on how much to spend on it. The economic theory of budget constraint is based on the assumption of weak separability between goods and services that leads tourists to allocate their budgets in accordance with a three-stage tourist spending process [8]: firstly, tourists decides how much of their budget to allocate for travel; secondly, they decide where to go on vacation; thirdly, they choose how to allocate their tourist budget among various goods and services offered by the selected destination. Obviously, these two economic theories are not disjointed but overlap; this means that an individual must make a two-stage decision process in each stage comprised in the three-stage tourist spending process. Since an in-depth knowledge of the determinants that affect tourist consumption behaviour is of primary importance for a destination [9], it is fundamental to accurately identify the set of factors that affect each stage of the decision-making process. In fact, the factors that determine tourism participation and tourism expenditure can be different and/or cannot have the same impact ([2], [10], [11]). At the same time, it is also fundamental to study the ways by which tourists choose a bundle of goods and services they consume/purchase at the destination to maximize their utility within certain budget constraints ([9], [12]). However, only few studies have analysed tourism expenditure behaviour by simultaneously considering both the consumer behaviour theory and the budget constraint theory ([13] [14]). Furthermore, many surveys conducted at either the national or international level, which investigate tourism expenditures, do not require proof (i.e., receipts) of expenditures, resulting in imprecise and vague information.

2.1 Real example data

The “International Tourism in Italy” survey, conducted annually by the Bank of Italy, has the aim of monitoring both travel expenditures and length of stay of inbound and outbound visitors from/to Italy determining the tourism balance of payments. The stratified sampling method is applied (using different types of stratified variables per each type of frontier) and face–to–face interviews are carried out at national borders (including highways, railway, airports, and harbours). Sampling is done independently at each type of frontier. Tourists are interviewed at the end of the trip when they are returning to their place of habitual residence and no proof of actual expenditure is required. Therefore, tourism expenditures provide imprecise and vague information since they reflect what tourists remember about their trip, which can be different from what was spent. Interviews are conducted at different times of the day, during both working days and holidays, and month by month, with a fixed number of interviews per each period of survey. The questionnaires are anonymous and are offered in 14 languages. Socio–demographic characteristics of the interviewee (such as age, occupation, and country of origin), information on the trip (such as travel group size) and information on travel expenditures are collected.

3. Literature review

3.1 The economic theories of tourists’ expenditure behaviour

Following the neoclassical economic theory of budget constraint, consumers are supposed to be rational and able to maximize their utility function by choosing among a set of available alternatives. Consumers are hence able to rank goods and services, so that they select the combinations from which their utility function gains the largest possible value, given budget and time constraints, relative prices, and preferences. Furthermore, the consumer’s utility function is assumed to be “separable”. The separability and the assumption of weak separability, only implies independence among broad aggregates of commodities, and not independence among individual commodities belonging to the same aggregate. It implies that the budgeting procedure by which individuals allocate their incomes among different goods and services is split in two stages [15]. Firstly, the individual decides in which broad commodity groups (i.e. food, tourism, housing, clothes, etc.) to allocate her/his income. Secondly, the individual decides which goods and services she/he wants to buy within each group, with no reference to expenditure in the other groups. Syriopoulos and Sinclair [8] applied this approach to the field of tourism suggesting a three-stage budgeting process. In the first stage, visitors allocate budget between the total tourism expenditure and the consumption of other goods and services. In the second stage, visitors allocate their tourist budget among different destinations, including the home country. Thirdly, visitors choose how to allocate their tourist budget among various goods and services offered by the selected destination. This means that the expenditure on different goods and services at the destination are dependent among each other but are independent of tourism expenditure for goods and services made in another destination.

In each stage of this tourism consumption budgeting process, the consumer firstly divides the set of goods and services into two categories: the goods and services that he/she wants to obtain and the group of goods and services in which he/she is not interested. Obviously, this decision depends on both economic factors, and non-economic factors (ethnicity, gender, psychological, etc.). Subsequently, the consumer will decide the amount of money that he/she is willing to pay for each good and service belonging to the desired group of products. Therefore, following the consumer choice theory, each decision-making process to purchase can be split in two stages, or decisions [7]: the decision to spend or not (the selection stage) and, if the consumer decides to spend, how much money to spend (the outcome stage).

3.2 Supervised Machine Learning algorithms

3.2.1 Modelling dependent information

As introduced in the previous paragraph, following the consumer choice theory, the decision-making process to purchase a tourism good or service can be schematically represented by a two-stage decision process. For this reason, the tourism literature has been devoted along the years to the study of each of these stages, both separately and jointly. The binary regression models, such as Logit and Probit models ([2], [10], [16], [17]) but also the more recent Scobit model [18], have been intensively used in order to find those variables that determine the probability, or propensity, to consume a specific tourism good or service (i.e. the selection stage). As regards the second stage, i.e. the outcome stage, the OLS method has been extensively used to estimate multiple regression models in which the dependent variable was the amount of money spent for a particular tourism expenditure category or for the whole trip (among others, see [5], [17]–[19]). More recently, the quantile regression model has been introduced in the tourism literature [1], [14], [20], [21]. The main advantage of the quantile regression model compared to the traditional OLS regression model is that it can identify the determinants of the whole distribution of the dependent variable, i.e., the tourism expenditure, instead of only the determinants of the average expenditure. The Tobit model, introduced by Tobin in the late 50s, has been the first model created with the aim to study simultaneously the two-stages of the decision-making process [22]. Along the years this model became quite common in the tourism literature [11], [23]–[27] but probably due to its lack in identifying separately the determinants of the two stages, the double-hurdle models, e.g. Cragg [28] and Heckman [29] models, have grown in popularity [30]–[36].

With the aim to incorporate the neoclassical economic theory of budget constraint in the study of the decision-making process, i.e. considering the dependence that might exist amongst alternative tourism expenditures on goods and services, two different system-of-equation approaches have been adopted in the tourism literature: the system of tobit equations [13], [37], [38]; and the almost ideal demand system (AIDS) model. The AIDS model, firstly introduced by Deaton and Muellbauer [15], has been commonly used to estimate the effect of relative prices and real expenditure on aggregate travel expenditures, but few studies have adopted this model also to estimate individual budget allocations of tourist expenditure for specific trips [14], [39] and to examine the third stage of the tourist budget allocation process [39]–[42]. Unfortunately, none of these systems of equations account for the imprecision of tourists’ expenditure.

3.2.2 Modelling imprecise information

The standard linear regression model is the most employed approach for assessing the cause-and-effect connection between a response variable and a set of predictor variables or covariates. However, when one or more of the involved variables (whether they are the response or predictors) are not precisely defined or accurately measured, the standard linear regression model proves inadequate in capturing the relationship between the response and predictor variables. In such cases, it becomes necessary to turn to the fuzzy regression model [43]–[46] and hence work in the framework of fuzzy set theory [47] and fuzzy numbers (see Remark 1).

Remark 1 Fuzzy numbers

The LR-type (Left and Right) fuzzy data is a general class of fuzzy data that can be defined in a matrix form as follows [48]:

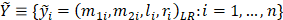
where is the LR fuzzy data observed on the ith unit; and (with ) represent the left and right centers of the fuzzy number, and represent the left and right spreads, i.e., the vagueness of the data. Once defined the general form of the fuzzy number, the membership function (see Remark 2) must be chosen [49].

Remark 2 Elicitation problem

The definition of the membership function (elicitation) and its specification are two important issues widely discussed in the literature [71]. The membership function is commonly developed based on expert’s capabilities and knowledge of the topic under investigation [72], [73]. The membership function is normally defined at macro level, i.e., the sample, rather than at individual level. In other words, the MF is defined equal and constant for a variable, regardless of individual characteristics, both physical, cultural and psychological, and question’s characteristics.

As per the comprehensive review conducted by Chukhrova and Johannssen [50], fuzzy regression analysis has seen substantial expansion and has gained increased importance in the field of fuzzy statistics, as confirmed by Li et al. [49]. In the literature, two main approaches to estimate a fuzzy regression model have been developed: the possibilistic and the fuzzy least squares approaches (refer to D’Urso [45], and Li et al., [49]). More recently, the Machine Learning approach has been added to these methods (as discussed in [50]). The possibilistic approach is based on the pioneering works of Tanaka et al [51]. The idea behind this method is to minimize the entire fuzziness (i.e., the vagueness of a phenomenon that cannot be expressed by randomness) of the predicted dependent variable by minimizing the total spread of the fuzzy parameters. This approach is known as possibilistic since the membership functions of fuzzy sets can be seen as possibility distributions. Since its introduction, this approach has been extensively used in applications, and several theoretical advancements have been suggested so far ([43], [52]–[55]). On the other hand, the least squares approach (firstly introduced by Celmiņš [56] and Diamond [57]) is an extension of the well-known least squares criterion. Therefore, its aim is to identify the linear model that best approximates the observed data in a metric space, in other words, the aim is to minimize the distance between the estimated fuzzy outputs and the observed fuzzy outputs using a suitable distance measure between fuzzy numbers. This approach has been extensively developed in the literature, as demonstrated by the large number of research papers published so far [43], [45], [49], [57]–[62]. Finally, the performance of the fuzzy regression has been enhanced by incorporating machine learning techniques, such as evolutionary algorithms, neural networks or support vector machines. See the extensive review of Chukhrova and Johannssen [50] for applications and developments of this approach.

3.4 Unsupervised Machine Learning algorithms

Cluster analysis is an unsupervised Machine Learning (ML) method used for conducting post hoc market segmentation. The primary objective of cluster analysis is to uncover concealed relationships among data points while grouping items to maximize similarity within groups and minimize dissimilarity between them. Given its exploratory nature, each clustering algorithm may yield a distinct partition for the same dataset. Consequently, there are not inherently right or wrong results; the utility of the outcomes depends on the compatibility of the clustering algorithm with the data's characteristics and requirements.

3.4.1 Clustering dependent information

According to Lee and Beeler [63] as well as Koc and Altinay [64], the development and maintenance of a competitive advantage in a highly competitive tourism markets hinge significantly on the degree to which visitors are well known and understood. Kau and Lim [65] emphasize that market segmentation enables destination planners to allocate resources more efficiently to attract distinct and unique groups of travellers. So, the process of market segmentation consists in the identification of groups of consumers that are similar for one or more behaviour, and then devises marketing strategies that appeal to one or more groups. Consequently, this kind of analysis can shed light on the existence of groups of tourists whose shared attitudes may lead to similar levels of spending and, consequently, a comparable economic impact on the region. In literature, research aiming to identify clusters of tourists who share the same expenditure behaviour can be found in [58]–[62], [66]–[68]. In all these articles, clustering analysis is performed considering different kind of expenditures as independent variables, i.e., without considering the dependence relationship that intrinsically characterise these kinds of data. To the best of our knowledge, no clustering algorithms for dependent variables, such as probabilistic clustering or copula-based clustering algorithms, have been suggested in the literature so far.

3.4.2 Clustering imprecise information

When imprecise information is used as segmentation variables in a clustering algorithm, a suitable distance measure must be adopted. Typically, imprecise information is converted into fuzzy numbers before being used in the clustering algorithm, and a distance measure for fuzzy data must be selected. For a discussion on fuzzy distance, you can refer to Coppi et al. [69]. Recent applications of clustering algorithms for fuzzy data can be found in [70] and [6].

4. Conclusions and future directions

Tourism expenditures are vague and imprecise information usually collected through national repeated-cross sectional surveys or dedicated surveys. To model such imprecise information, Fuzzy set theory can be adopted. Practically, tourism expenditures can be converted into fuzzy numbers before the implementation of either a fuzzy regression model or a clustering algorithm using fuzzy distance. Since the imprecision by which tourists give information about their expenditures can be assumed to be a function of both length of stay (the longer the holiday, the higher the imprecision) and amount of money spent at the destination (the higher the expenditure, the higher the imprecision), a new method to compute the latent individual imprecision of the fuzzy number must be investigated.

According to the economic theory of budget constraint, tourists generally allocate their budget following to a three-stage process [8]. This theory assumes the principle of weak separability among goods and services: expenditures on different goods and services belonging to the same category (i.e. travel) are dependent on each other while broad aggregates of commodities are independent among them. Moreover, expenditures are generally characterised by a high level of zero values. The dependence among censored variables (hence tourism expenditures) should be further investigated and the applicability of either suitably Copula functions should be analysed.

Finally, to the best of our knowledge, no clustering algorithm has been developed so far to identify group of visitors with similar expenditure behaviour at the destination accounting for both the imprecision of data collected and the dependence among different expenditure categories. Therefore, there is a need in developing adequate clustering algorithms for dependent and imprecise information.

Concluding, we emphasize that imprecise information and dependent information have been extensively analysed in the literature, bridging from econometric modelling to machine learning algorithms. However, to the best of our knowledge, these kinds of information have been studied mostly separately, and no methods have been implemented so far to analyse information that is both dependent and imprecise.

ACKNOWLEDGMENTS

This study was carried out within the MOST—Sustainable Mobility National Research Centre and received funding from the European Union Next-GenerationEU (PIANO NAZIONALE DI RIPRESA E RESILIENZA (PNRR)—MISSIONE 4 COMPONENTE 2, INVESTIMENTO 1.4—D.D. 1033 17 June 2022, CN00000023). This manuscript reflects only the authors’ views and opinions, neither the European Union nor the European Commission can be considered responsible for them.

References